Цилиндрические зубчатые передачи.

Достоинства зубчатой передачи: высокая нагрузочная способность, надежность, долговечность; высокий КПД; постоянство передаточного отношения; малые силы.

Недостатки зубчатой передачи: высокие требования к точности изготовления и монтажа; отсутствие компенсации динамических нагрузок; шум при работе с большими скоростями; отсутствие предохранения при перегрузках.

Передаваемые мощности зубчатой передачи до 10000 кВт, линейная скорость до 150 м/с, размеры от долей мм до десятков метров.

На зубчатые передачи установлены 12 степеней точности по ГОСТ 1643-81, характеризующие кинематическую точность колес, плавность их работы, пятно контакта и боковой зазор. Выбор степени точности зависит от назначения и условий работы зубчатой передачи. Так для редукторов общего назначения назначают 6...9 степени точности, для металлорежущих станков - 5...6; легковых автомобилей - 5...8; грузовых - 7...9.

Зубчатая передача, в которой образующие боковых поверхностей зубьев параллельны образующим делительного цилиндра шестерни и колеса, называется прямозубой цилиндрической передачей. Наиболее важным элементом зубчатых колес являются боковые рабочие поверхности зубьев, воспринимающие нагрузки при работе передачи, когда зубья одного колеса входят во впадины другого.

3.6.1 Геометрия прямозубых зубчатых колес (основные параметры).

Основные параметры зубчатых колес представлены на рисунке 71.

Окружности, касающиеся друг друга в полюсе зацепления (т. П, рисунок 71), имеющие общие с зубчатыми колесами центры и перекатывающиеся одна по другой без скольжения, называют начальными: d_w. Окружность, на которой шаг Р и угол зацепления a_w соответствуют шагу и углу профиля инструментальной рейки называется делительной: d. Для зубчатого зацепления без смещения d_w = d.

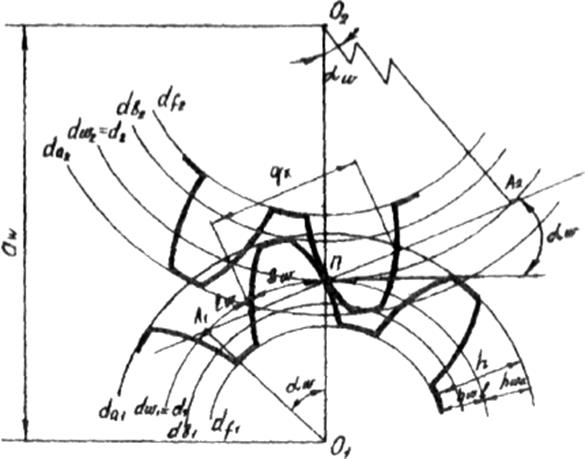
Рис 71.

Шаг зубьев - расстояние между одноименными профилями двух соседних зубьев, взятое по дуге делительной окружности:

, где l_w - длина впадины, S_w - толщина зуба.

Длина делительной окружности должна быть такой, чтобы на ней умещалось целое число зубьев z, т.е.

, откуда .

Линейная величина в π раз меньше шага называется окружным модулем зубчатого зацепления: m - основной параметр зубчатой передачи; согласно ГОСТ 9563-80 m = 1,5...11 мм.

Диаметры начальных и делительных окружностей:

; .

На делительной окружности толщина зуба S_w равна ширине впадины l_и. Межосевое расстояние:

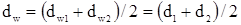
Делительная окружность рассекает зуб по высоте на головку h_a и ножку h_f: h_a = m; h_f = 1,25 m.

Высота зуба: .

Радиальный зазор: .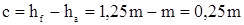

Диаметры окружностей вершин или выступов:

;

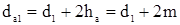Окружности впадин:

;

Основные окружности:

;

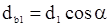где α = 20° - угол зацепления - угол, образованный линией зацепления А₁А₂ и обшей касательной, проведенной через полюс зацепления к делительным (начальным) окружностям шестерни и колеса. Линия зацепления А, А, - это линия, по которой направлена сила давления зуба ведущего колеса на точку боковой поверхности зуба ведомого колеса в процессе зацепления их.

В настоящее время широкое распространение получили косозубые передачи, у которых зубья расположены по винтовой линии на делительном цилиндре. В отличие от прямозубой передачи в косозубой зубья входят в зацепление не сразу по всей длине, а постепенно, что значительно снижает шум и динамические нагрузки, повышая нагрузочную способность передачи.

Для нарезания косых зубьев используют тот же инструмент, что и прямых. Наклон зуба образуют поворотом инструмента относительно заготовки на угол β - угол наклона зубьев (8°-15°). В этой передаче различают нормальный стандартный модуль m_n - модуль в нормальном сечении и торцевой (окружной) модуль m_t = m_n/cosβ, который определяют с точностью до 3 знаков.

При определении основных параметров косозубой передачи необходимо учесть, что диаметры начальных (делительных) окружностей определяют по формулам:

.;

Остальные геометрические размеры определяют аналогично прямозубым.

3.6.2 Силы, действующие в зацеплении.

Пренебрегают силами трения и считают, что сила нормального давления F_n приложена в полюсе зацепления и направлена по линии зацепления, как общей нормали к рабочим поверхностям зубьев. Эта сила является равнодействующей окружной F_t и радиальной F_r сил (Рисунок 72).

, ,

откуда ; _;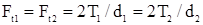

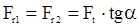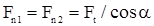
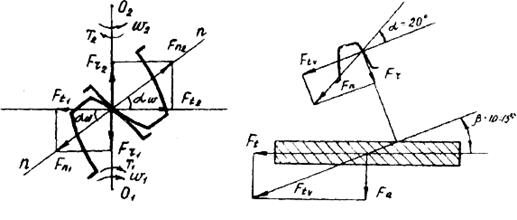
_{Рис 72.}

ёНедостатком косозубых колес является наличие осевой силы в зацеплении. Прочность зуба определяют его размеры и форма в нормальном сечении, причем форму косого зуба в нормальном сечении принято определять через параметры приведенного (эквивалентного) прямозубого колеса, диаметр которого: , (Рисунок 72).

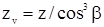- эквивалентное число зубьев приведенного колеса. Окружная сила приведенного колеса: .

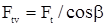Силы в косозубом зацеплении:

;

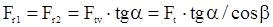
3.6.3 Расчет цилиндрических передач на выносливость по контактным напряжениям.

Основным критерием работоспособности закрытых передач является контактная прочность рабочих поверхностей зубьев. Поэтому основные размеры этих передач определяются из проектного расчета по контактным напряжениям. Цель расчета: предупредить выкрашивание рабочих поверхностей зубьев. При расчете контактных напряжений рассматривают соприкосновение зубьев в полюсе, где происходит их зацепление. Напряжения в высшей кинематической паре распределены по эллиптическому закону аналогично контакту двух цилиндров радиусами р₁ и р₁ (Рисунок 73).

σ_max – для цилиндрических поверхностей определяются по формуле Герца-Беляева

,

где μ = 0,3 - коэффициент Пуассона для стали.

Рис 73.

- интенсивность нормальной силы (удельная нагрузка на единицу длины).

Сила нормального давления ;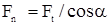

- суммарная длина контактных линий;

b - длина зуба;

К_с - коэффициент, учитывающий форму сопряженных поверхностей;

ε_α - коэффициент торцевого перекрытия.

- приведенный модуль упругости, учитывающий материал обоих колес.

- приведенный радиус кривизны. Подставив в формулу Герца выражение, определяющее интенсивность нормальной силы, а также коэффициенты, учитывающие форму сопряженных поверхностей зубьев, коэффициенты учитывающие механические свойства материала и суммарную длину контактных линий для стальных цилиндрических зубчатых колес получим формулу проверочного расчета передач на выносливость по контактным напряжениям:

,

где С = 310 - для прямозубых колес, и С = 270 для косозубых колес.

К_н - коэффициент нагрузки, учитывающий реальные условия работы колес: ;

K_нα- коэффициент, учитывающий неравномерность распределения нагрузки между зубьями, зависит от точности изготовления, для прямозубых колес , для косозубых выбирают по таблицам;

К_нβ - коэффициент неравномерности нагрузки по ширине колеса, зависит от прогиба валов и перекоса зубчатых колес;

из таблиц или графиков;

К_нv - коэффициент динамической нагрузки, выбирают из таблиц в зависимости от окружной скорости, точности изготовления и твердости колес: .

Для предварительных расчетов принимают К_н = 1,2...1,5.

Величина расчетных контактных напряжений одинакова для шестерни и колеса. Расчет выполняется для того из колес, у которого меньше допускаемое напряжение [σ]_н (в большинстве случаев для колеса).

K_нL - Коэффициент долговечности =1 для общего редукторостроения;

S_н - коэффициент безопасности = 1,1 ... 1,2;

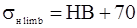- предел контактной выносливости при базовом числе циклов.

При проектном расчете необходимо определить размеры передачи - a_w. Исключим из формулы линейный параметр b.

Обозначим b/a_w = ψ_ba- коэффициент ширины колеса относительно межосевого расстояния, для редукторов ,

тогда 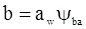, возведем в квадрат вышеприведенное неравенство

,

отсюда межосевое расстояние a_w равно:

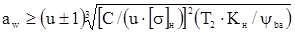,мм

- формула для проектного расчета цилиндрических передач на выносливость по контактным напряжениям. Величина а уточняется по ГОСТ 2185-66. Знак "+" для внешнего зацепления, "-" для внутреннего.

Основной параметр - m для зубчатых колес выбирается: m = (0,01...0,02) • а_w, мм и уточняется по ГОСТ 9563-80, для редукторов m > 2...1,5 мм. Суммарное число зубьев колес:

;

число зубьев шестерни:

_;

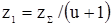число зубьев колеса:

.

3.6.4 Расчет цилиндрических передач на выносливость по напряжениям изгиба.

Если расчет зубчатых закрытых передач на контактную прочность выполняется как проектный, то расчет на выносливость зубьев по напряжениям изгиба выполняется как проверочный. Для открытых зубчатых передач расчет зубьев на изгиб является основным. Цель - предотвращение усталостных поломок зубьев.

1) Примем, что в зацеплении находится одна пара зубьев;

2) Сила нормального давления приложена к вершине зуба;

3) Силами трения пренебрегают, т.к. они малы. В этом случае зуб можно представить как балку, защемленную по дуге А В.

От силы F_t волокна в точке В растягиваются. В точке А - сжимаются.

Рис 74.

От силы F₁ - волокна во всех точках сжимаются (Рисунок 74).

Усталостные трещины возникают на растянутой стороне - у точки В. Зубья рассчитываются по результирующему напряжению σ_F, возникающему на рабочей грани зуба, и равному разности между изгибающим и сжимающим напряжениям: .