Конические зубчатые передачи
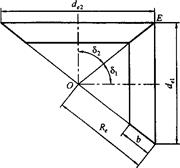 Конические зубчатые передачи передают механическую энергию между валами с пересекающимися осями (рис.3.1,е,ж,з, 3.10). Получили распространение в редукторах общего назначения и металлообрабатывающих станках. Зацепление двух конических колес можно представить как качение без скольжения конусов с углами при вершинах
Конические зубчатые передачи передают механическую энергию между валами с пересекающимися осями (рис.3.1,е,ж,з, 3.10). Получили распространение в редукторах общего назначения и металлообрабатывающих станках. Зацепление двух конических колес можно представить как качение без скольжения конусов с углами при вершинах 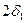 и
и 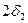 . Эти конусы называются начальными. Линия касания этих конусов ОЕ называется полюсной линией, или мгновенной осью, в относительном вращении колес. Основное применение получили ортогональные передачи с суммарным углом между осями
. Эти конусы называются начальными. Линия касания этих конусов ОЕ называется полюсной линией, или мгновенной осью, в относительном вращении колес. Основное применение получили ортогональные передачи с суммарным углом между осями 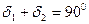 .
.
Конические зубчатые передачи выполняются без смещения исходного контура. 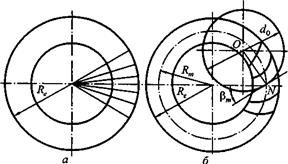 Конические колеса (рис.3.11) выполняют прямозубыми, с тангенциальными и круговыми зубьями. Прямозубые передачи применяют при окружных скоростях до 3 м/с, в прямозубых с повышенной точностью —до 8 м/с. При более высоких скоростях применяют передачи с круговыми зубьями.
Конические колеса (рис.3.11) выполняют прямозубыми, с тангенциальными и круговыми зубьями. Прямозубые передачи применяют при окружных скоростях до 3 м/с, в прямозубых с повышенной точностью —до 8 м/с. При более высоких скоростях применяют передачи с круговыми зубьями.
| Рис.3.11 Форма линий зуба конического колеса: а — с прямыми зубьями; б — с круговыми зубьями |
Геометрические параметры.Углы делительных конусов связаны с их диаметрами и числами зубьев z

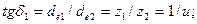 (3.14)
(3.14)
где и= 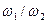 — передаточное отношение, равное передаточному числу
— передаточное отношение, равное передаточному числу 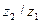 .
.
Внешние делительные диаметры колес равны
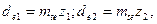 (3.15)
(3.15)
где mte —окружной модуль зацепления на торце.
Внешнее конусное расстояние Re равно
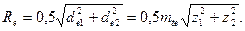 (3.16)
(3.16)
Расчеты на прочность ведут в сечении где среднее конусное расстояние
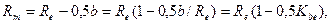 (3.17)
(3.17)
где 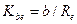 — коэффициент ширины зубчатого венца.
— коэффициент ширины зубчатого венца.
Значение 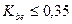 (обычно 0,285).
(обычно 0,285).
Средний делительный диаметр и модуль находят из соотношений
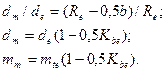 (3.18)
(3.18)
Диаметр вершин зубьев равен
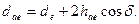
| Рис.3.12 Основные параметры конического зубчатого колеса |
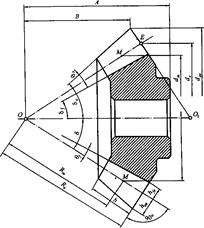 Эквивалентное зубчатое колесо, эквивалентное число зубьев. При качении без скольжения плоскости по основному конусу точки прямой (например, ОЕ) опишут эвольвентную коническую поверхность зуба. Точка Е опишет эвольвенту на поверхности шара радиусом
Эквивалентное зубчатое колесо, эквивалентное число зубьев. При качении без скольжения плоскости по основному конусу точки прямой (например, ОЕ) опишут эвольвентную коническую поверхность зуба. Точка Е опишет эвольвенту на поверхности шара радиусом 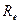 . Эвольвентное сферическое зацепление описать аналитически, а также изготовить его чрезвычайно сложно. На практике сферическую поверхность заменяют касательной конической поверхностью, образующие которой нормальны к делительному конусу
. Эвольвентное сферическое зацепление описать аналитически, а также изготовить его чрезвычайно сложно. На практике сферическую поверхность заменяют касательной конической поверхностью, образующие которой нормальны к делительному конусу 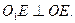 Эту поверхность называют дополнительным делительным конусом. Профиль зубьев на развертке дополнительного конуса отличается от эвольвентного, так как высота зуба мала по сравнению с длиной Re. Профиль зубьев на дополнительном конусе будет соответствовать эквивалентному цилиндрическому зубчатому колесу диаметром, равным
Эту поверхность называют дополнительным делительным конусом. Профиль зубьев на развертке дополнительного конуса отличается от эвольвентного, так как высота зуба мала по сравнению с длиной Re. Профиль зубьев на дополнительном конусе будет соответствовать эквивалентному цилиндрическому зубчатому колесу диаметром, равным
dv=2OlE = de/cos8. (3.19)
Эквивалентное число зубьев из зависимости 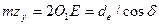 равно
равно
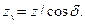
Для передач с круговыми зубьями по аналогии с цилиндрическими передачами
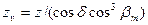 (3.20)
(3.20)
Исходный контур конических зубчатых колес.Коническое колесо конической передачи, которая имеет угол начального конуса 2δ=180° называется плоским (рис.3.3,г,д,е). Конические колеса с прямыми зубьями и внешним окружным модулем те>1 мм выполняют по ГОСТ 13754-81 со следующими параметрами (рис.3.3): α=20°, ha*=1, С*=0,2, ρf=0,2 (угол профиля, коэффициент высоты головки и ножки зуба, коэффициент радиального зазора и радиуса скругления).
Согласно ГОСТ .16202-81 — для конических колес с круговыми зубьями с модулем в нормальном сечении тn>1 мм, параметрами αn=20°, ha*=1, С* - 0,25, ρf =0,25. Нормальное расчетное сечение и угол наклона βn выбирают на расстоянии Rm .
Осевая форма зуба.Назначается при проектировании и в некоторой степени связана с диаметром d0 резцовой головки. Диаметры резцовых головок стандартизованы.
Осевая «форма 1» (рис.3.13,а) — пропорционально понижающиеся зубья. Вершины конусов делительного и впадин совпадают. Эту форму применяют для прямых и круговых зубьев с тп≤2,5 мм.
Осевая «форма 2» (рис.3.13,б,в) — вершины конусов не совпадают и располагаются так, что ширина дна впадины колеса постоянна. Это позволяет обрабатывать одним резцом обе поверхности зубьев впадины, не раздвигая резцы при настройке станка. Эта осевая форма зубьев является основной для круговых зубьев с модулями тп=0,4...25 мм, zc≥24.
Осевая «форма 3» (рис.3.13,г) — равновысокие зубья. Образующие конусов делительного, вершин и впадин зубьев параллельны. Высота зуба постоянна по всей длине. Эту форму применяют для тп=2...25, zc ≥40.
Геометрический расчет.Зависит от зацепления колес, измерительных размеров, от осевой формы зубьев. Основные геометрические параметры приведены выше.
Угол наклона зубьев. Назначается на среднем конусном расстоянии. Увеличение угла наклона повышает плавность работы, но увеличивает осевую нагрузку на опоры валов. Преимущественно применяют βm=35°.
Передаточное число и число зубьев. Понижающие конические передачи выполняют с передаточным числом и=1...10. Повышающие — не более 3. Большие передаточные числа усложняют конструирование шестерни и ее узла подшипников. Обычно и<6.
Число зубьев шестерни следует выбирать больше минимально допустимого числа ее зубьев по рис.3.14 и табл. 3.5.
Таблица 3.5 Минимально допустимые числа зубьев шестерни
| Передаточное число и | z1 при β° | |
| 1,6 | ||
| ≥3,15 |
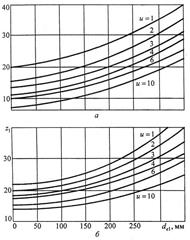 При этом передачи получаются равнопрочными по контактным и изгибным напряжениям.
При этом передачи получаются равнопрочными по контактным и изгибным напряжениям.
Число зубьев колеса z2=z1u . При окончательном выборе следует учесть рекомендацию по числу зубьев zc плоского колеса.
 Коэффициенты смещения. Для равносмещенной передачи принимают у шестерни положительное смещение, у колеса—отрицательное, равное по абсолютной величине х2=-х1,
Коэффициенты смещения. Для равносмещенной передачи принимают у шестерни положительное смещение, у колеса—отрицательное, равное по абсолютной величине х2=-х1,
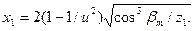
Для прямозубых колес cosβm=1.
Для достижения равнопрочности по изгибу зубьев колес увеличивают расчетную толщину зуба шестерни, а у колеса уменьшают на такую же величину посредством разведения резцов. Коэффициент тангенциального смещения, характеризующий изменение толщины зуба при и>2,5, определяют по формуле
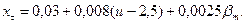
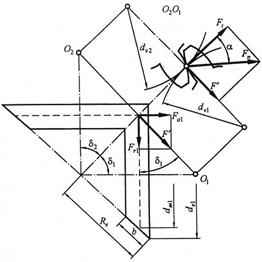 Силы в зацеплении.Результирующую силу Fn, действующую в нормальной плоскости к поверхности зуба, раскладываем на составляющие: окружную Ft, радиальную Fr и осевую Fa. Известен вращающий момент Т, Н·м, и следовательно, известна окружная сила на среднем делительном диаметре. Выразим через окружную силу другие составляющие (рис.3.15, сечение О2О1)
Силы в зацеплении.Результирующую силу Fn, действующую в нормальной плоскости к поверхности зуба, раскладываем на составляющие: окружную Ft, радиальную Fr и осевую Fa. Известен вращающий момент Т, Н·м, и следовательно, известна окружная сила на среднем делительном диаметре. Выразим через окружную силу другие составляющие (рис.3.15, сечение О2О1)
Дата добавления: 2015-07-18; просмотров: 2060;
