Расчет прямозубых цилиндрических передач на прочность
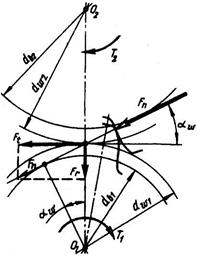 Расчет на прочность прямозубых и косозубых цилиндрических передач стандартизован ГОСТ 21354—87. Силы в зацеплении. На рис.3.5 Fn — нормальная сила, направленная по линии зацепления как общей нормали к рабочим поверхностям зубьев. Силы, действующие в зацеплении, принято прикладывать в полюсе зацепления. При этом силу Fn переносят в полюс и раскладывают на окружную Ft и радиальную Fr. По заданным Т и d определяют
Расчет на прочность прямозубых и косозубых цилиндрических передач стандартизован ГОСТ 21354—87. Силы в зацеплении. На рис.3.5 Fn — нормальная сила, направленная по линии зацепления как общей нормали к рабочим поверхностям зубьев. Силы, действующие в зацеплении, принято прикладывать в полюсе зацепления. При этом силу Fn переносят в полюс и раскладывают на окружную Ft и радиальную Fr. По заданным Т и d определяют
Ft=2T1/dw1≈2T1/d1 (3.1)
и через нее выражают все другие составляющие:
Fr=Fttgαw, Fп=Ft/cosαw. (3.2)
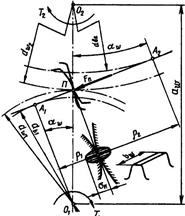
 Расчет прочности зубьев по контактным напряжениям. Расчет контактных напряжений выполняют при контакте в полюсе зацепления (рис.3.6). Контакт зубьев рассматривают как контакт двух цилиндров с радиусами ρ1 и ρ2. Контактные напряжения определяют по формуле:
Расчет прочности зубьев по контактным напряжениям. Расчет контактных напряжений выполняют при контакте в полюсе зацепления (рис.3.6). Контакт зубьев рассматривают как контакт двух цилиндров с радиусами ρ1 и ρ2. Контактные напряжения определяют по формуле:
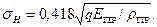 (3.3)
(3.3)
Для прямозубых передач
q=FnKH/bw=FtKH/(bwcosaw)=2T1KH/(dw1bwcosaw).(3.4)
Радиусы кривизны эвольвент зубьев в точке контакта
 ρ1=(dw1sinaw)/2; ρ2=(dw2 sinaw)/2.
ρ1=(dw1sinaw)/2; ρ2=(dw2 sinaw)/2.
По формуле,
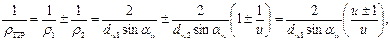 (3.5)
(3.5)
где u=dw2/dwl=z2/z1 знак «+»— для наружного, а «—»—для внутреннего зацепления.
Подставляя в формулу (3.3) и заменяя cosαwsinαw=(sin2αw)/2, получаем
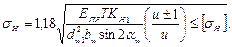 (3.6)
(3.6)
Параметр u=z2/z1 по ГОСТ 16532—70 передаточное число определяют как отношение большего числа зубьев к меньшему. Передаточное число отличается от передаточного отношения i, которое, равно отношению угловых скоростей ведущего колеса к ведомому и которое может быть меньше или больше единицы, положительным или отрицательным. Применение и вместо i связано с принятой формой расчетных зависимостей для контактных напряжений, где ρпр выражено через d1, а не через d2. Значение контактных напряжений, так же как и значение передаточного числа и, не зависит от того, какое колесо ведущее, а значение передаточного отношения i зависит. Передаточное число и относится только к одной паре зубчатых колес. Его не применяют для обозначения передаточного отношения многоступенчатых редукторов, планетарных, цепных, ременных и других передач. Значения расчетных контактных напряжений одинаковы для шестерни и колеса. Расчет выполняют для колеса, у которого чаще меньше допускаемое напряжение [σН].
Неизвестные параметры оценивают приближенно или выбирают по рекомендациям на основе накопленного опыта. Принимаем dw1≈d1; αw≈α=20°(sin2α≈0,6428), KHv≈1,15 коэффициент зависит от окружной скорости v, которая пока неизвестна, поэтому принято некоторое среднее значение. При этом из составляющих коэффициента Кн остается только КНβ. Далее обозначаем ψbd=bw/dl — коэффициент ширины шестерни относительно диаметра.
Подставляя в формулу (3.6) и решая относительно d1, находим
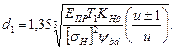 (3.7)
(3.7)
Решая относительно межосевого расстояния а, заменяем Т1=Т2/и; d1=2a/(u±1) и вводим ψba=bw/а—коэффициент ширины колеса относительно межосевого расстояния.
После преобразований с учетом зависимости
ψbd=0,5 ψba(и±1) . (3.8)
получим
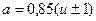
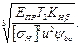 (3.9)
(3.9)
В приложении к ГОСТ 21354—87 для стальных зубчатых колес формулы (8.7) и (8.9) записаны в виде
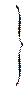
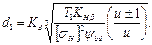 (3.10)
(3.10)
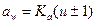
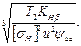
где Kd и Ка — вспомогательные коэффициенты, полученные в результате выноса числового значения Епр из под знака радикала, в формулах разные единицы одинаковых физических величин; Т—в Н·м, d и а — в мм, σН—в МПа.
Для стальных прямозубых колес Kd=780(МПа)1/3, Ка=490 (МПа)1/3, для косозубых Kd=680 (МПа)1/3, Ка=430 (МПа)1/3.
Выбор модуля и числа зубьев. Значение т выбирают, ориентируясь на рекомендации, выработанные практикой, и затем проверяют на изгиб. Минимальное значение модуля определяют из условия прочности зубьев на изгиб. При этом расчете в большинстве случаев получают зацепления с мелкими зубьями, применение которых ограничено. Значение контактных напряжений σH не зависит от модуля или числа зубьев, а определяется их произведением или диаметрами колес. По условиям контактной прочности при d1 модуль передачи может быть любым, при соблюдении равенства mz1=dl.
Крупномодульные колеса могут работать длительное время после начала выкрашивания, менее чувствительны к перегрузкам и неоднородности материала. При ориентировочной оценке значения т можно использовать рекомендации табл. 3.4.
Выбрав по этой таблице ψт, определяют
т= bw/ψт, (3.11)
где
bw=ψbdd1=ψbaa. (3.12)
Таблица 3.4
| Конструкция | ψт=bw/m, не более |
| Высоконагруженные точные передачи, валы, опоры и корпуса повышенной жесткости: | |
| Н≤350HB | 45...30 |
| Н>350НВ | 30...20 |
| Обычные передачи редукторного типа в отдельном корпусе с достаточно жесткими валами и опорами (и другие аналогичные): Н≤350HB | 30...20 |
| Н>350НВ | 20..15 |
| Грубые передачи, например с опорами на стальных конструкциях (крановые и т.п.) или с плохо обработанными колесами (литые), а также открытые передачи, передачи с консольными валами (конические), подвижные колеса коробок скоростей | 15...10 |
Примечание. Меньшие значения ψт — для повторно-кратковременных режимов работы, значительных перегрузок и средних скоростей; большие значения ψт — для длительных режимов работы, небольших перегрузок и высоких скоростей.
Значение т согласуют со стандартом (табл. 3.1). Для силовых передач обычно рекомендуют принимать т ≥1,0 мм. При известном модуле определяют и уточняют все остальные параметры передачи.
Для передач без смещения и при xΣ=0
d1=2a/(u±l); z1=d1/m; z2=zlu; d2= mz2; a=0,5(d2±d1). (3.13)
Должно быть zl>zmin, где zmin—по табл. 8.6.
Для уменьшения шума в быстроходных передачах рекомендуют брать z1≥25. Для окончательного значения модуля необходимо проверить прочность по напряжениям изгиба. В случае неудовлетворительного результата изменяют т и определяют новые значения z.
При проверке можно получить σF значительно меньше [σF], что не является противоречивым или недопустимым, так как нагрузочная способность большинства передач ограничивается контактной прочностью, а не прочностью на изгиб. Если расчетное значение σF превышает допускаемое, то применяют колеса, нарезанные с положительным смещением инструмента, или увеличивают т. В такой передаче решающее значение имеет прочность на изгиб. На практике такие случаи встречаются у колес с высокотвердыми зубьями при Н>50...60HRC (цементированные зубья).
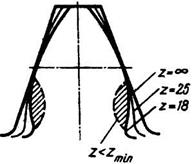 Влияние числа зубьевна форму и прочность зубьев. На рис.3.7 показано изменение формы зуба в зависимости от числа зубьев колес, нарезанных без смещения с постоянным модулем. При z→∞ колесо превращается в рейку, и зуб приобретает прямолинейные очертания. С уменьшением z уменьшается толщина зуба у основания и вершины, а также увеличивается кривизна эвольвентного профиля. Такое изменение формы приводит к уменьшению прочности зуба. При дальнейшем уменьшении z появляется подрезание ножки зуба (штриховая линия на рис. 3.7), прочность зуба существенно снижается.
Влияние числа зубьевна форму и прочность зубьев. На рис.3.7 показано изменение формы зуба в зависимости от числа зубьев колес, нарезанных без смещения с постоянным модулем. При z→∞ колесо превращается в рейку, и зуб приобретает прямолинейные очертания. С уменьшением z уменьшается толщина зуба у основания и вершины, а также увеличивается кривизна эвольвентного профиля. Такое изменение формы приводит к уменьшению прочности зуба. При дальнейшем уменьшении z появляется подрезание ножки зуба (штриховая линия на рис. 3.7), прочность зуба существенно снижается.
 При нарезании инструментом реечного типа для прямозубых передач число зубьев на границе подрезания zmin=17.
При нарезании инструментом реечного типа для прямозубых передач число зубьев на границе подрезания zmin=17.
Рассмотренное влияние числа зубьев на прочность справедливо при постоянном модуле, когда с увеличением z увеличиваются и диаметры колес. При постоянных диаметрах с изменением z изменяется модуль т. В этом случае изменяются не только форма, но и размеры зуба. С увеличением z форма улучшается, а размеры уменьшаются. Уменьшение модуля снижает прочность зуба на изгиб.
 Смещение инструментапри нарезании зубьев и его влияние на форму и прочность зубьев. На рис. 3.8 изображено два положения инструмента (рейки) при нарезании зубьев: 1— делительная плоскость
Смещение инструментапри нарезании зубьев и его влияние на форму и прочность зубьев. На рис. 3.8 изображено два положения инструмента (рейки) при нарезании зубьев: 1— делительная плоскость 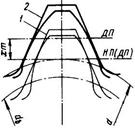 рейки (ДП) совпадает с начальной плоскостью (НП)— нарезание без смещения; 2—инструменту дано положительное смещение хт. При этом основной db и делительный d диаметры колеса не изменяются, так как не изменяется z (НП по-прежнему обкатывается по d, а ДП смещена на хт). Как видно из чертежа, смещение инструмента вызвало значительное изменение формы зуба. Толщина зуба у основания увеличилась, увеличилась и прочность зуба по напряжениям изгиба. Одновременно с этим заострилась головка зуба. Заострение является одной из причин, ограничивающих значение смещения инструмента. Отрицательное смещение инструмента сопровождается явлениями обратного характера.
рейки (ДП) совпадает с начальной плоскостью (НП)— нарезание без смещения; 2—инструменту дано положительное смещение хт. При этом основной db и делительный d диаметры колеса не изменяются, так как не изменяется z (НП по-прежнему обкатывается по d, а ДП смещена на хт). Как видно из чертежа, смещение инструмента вызвало значительное изменение формы зуба. Толщина зуба у основания увеличилась, увеличилась и прочность зуба по напряжениям изгиба. Одновременно с этим заострилась головка зуба. Заострение является одной из причин, ограничивающих значение смещения инструмента. Отрицательное смещение инструмента сопровождается явлениями обратного характера.
Применяют два типа передач со смещением:
1. Шестерню изготовляют с положительным смещением (x1>0), колесо—с отрицательным (х2<0), но так, что
|x1|=|x2| или хΣ=х1+х2=0.
При любом смещении сумма ширины впадины и толщины зуба по делительной окружности равна шагу р. Одинаковые по значению, но разные по знаку смещения вызывают одинаковые увеличения толщины зуба шестерни и ширины впадины колеса. Поэтому в зацеплении зубчатой пары при хΣ=0 делительные окружности соприкасаются и являются начальными, как в передаче без смещения. Не изменяются также межосевое расстояние aw и угол зацепления αw:
aw=a=0,5(d1+d2); αw=α=20°.
Изменяется только соотношение высот головок и ножек зубьев.
2. Суммарное смещение хΣ не равно нулю. Обычно хΣ>0,а также х1>0 и х2>0. При положительных x1 и х2 делительная толщина зубьев шестерен и колеса больше р/2. Поэтому делительные окружности не могут соприкасаться. Начальными становятся новые окружности, большие, чем делительные (dw1>d1, dw2>d2). Межосевое расстояние увеличивается:
aw=0,5(dw1+dw2)>а=0,5(d1+d2).
При этом увеличивается и угол наклона линии зацепления как общей касательной к основным окружностям, т.е. увеличивается угол зацепления: αw>α=20°. Увеличение αw сопровождается уменьшением коэффициента перекрытия εа, что является отрицательным и служит одной из причин, ограничивающих применение больших смещений. Нарезание со смещением позволяет повысить качество зубчатого зацепления.
1. Положительное смещение повышает прочность зубьев на изгиб и устраняет подрезание при малом числе зубьев (понижает zmin). Например, при z=25 увеличение х от нуля до +0,8 уменьшает YFS в 1,2 раза. Соответственно уменьшаются и напряжения изгиба σF. Можно понизить zmin от 17 до 8.
2. Увеличение αw при xΣ>0 повышает контактную прочность. Увеличение αw до 25° позволяет увеличить допускаемую нагрузку до 20%.
3. При большом числе зубьев у шестерни и колеса смещение малоэффективно, так как форма зуба при значительных смещениях не изменяется. Передачи со смещением при xΣ=0 применяют при больших и и малых z1. В этих условиях смещения х1>0 и х2<0 выравнивают форму зубьев шестерни и колеса и приближают их к равнопрочности по изгибу.
| Рис.3.9 Конструкция зубчатых колес. |
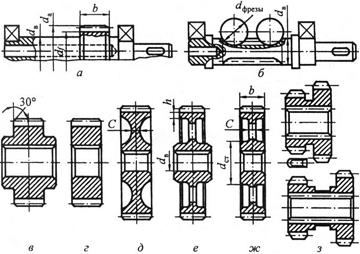 Конструкция зубчатых колеспоказана на рис.3.9. Шестерни с диаметром впадин df, близким к диаметру вала dВ, изготовляют заодно с валом (рис.3.9,а,б). Шестерни и колеса небольшого диаметра (dа≤200 мм) выполняют в виде дисков со ступицами или без ступиц (рис.3.9,в,г). В коробках передач применяют блоки шестерен (рис.3.9,з). Зубчатые колеса и блоки шестерен в зависимости от серийности производства изготовляют штамповкой, ковкой или точением из прутка. Коэффициент использования металла при точении шестерен из прутка равен в среднем 3, при штамповке в закрытых штампах он в 2 раза выше.
Конструкция зубчатых колеспоказана на рис.3.9. Шестерни с диаметром впадин df, близким к диаметру вала dВ, изготовляют заодно с валом (рис.3.9,а,б). Шестерни и колеса небольшого диаметра (dа≤200 мм) выполняют в виде дисков со ступицами или без ступиц (рис.3.9,в,г). В коробках передач применяют блоки шестерен (рис.3.9,з). Зубчатые колеса и блоки шестерен в зависимости от серийности производства изготовляют штамповкой, ковкой или точением из прутка. Коэффициент использования металла при точении шестерен из прутка равен в среднем 3, при штамповке в закрытых штампах он в 2 раза выше.
Колеса средних диаметров с dа≤600 мм выполняют кованными облегченной конструкции (рис.3.9,д,е,ж). Толщину обода h улучшенных колес выбирают равной (2…3)m, толщину дисков С=(0,2…0,3)b, диаметры ступиц – dст=(1,6…1,9)dВ (где b ширина колеса, dВ- диаметр вала). Технологичная конструкция штампованного колеса показана на рис.3.9,д (диск С механически обрабатывается).
Колеса цельнолитые менее трудоемки, но по нагрузочной способности не уступают колесам кованым. Их применяют при больших диаметрах и нежестких требованиях к габаритным размерам. Иногда используют колеса, у которых зубчатый венец соединяют с диском и ступицей болтами.
Тихоходные зубчатые колеса изготавливают из чугуна или углеродистой стали.
Быстроходные – из легированной стали. Для увеличения прочности и повышения стойкости зубчатых колес против износа подвергают термической обработке после нарезания зубьев на зубонарезных станках. Поверхность зубьев колес из углеродистой стали, улучшают химико-термическим способом – цементацией и потом закалкой. Зубья быстроходных колес после термической обработки шлифуют или притирают. Применяется поверхностная закалка токами высокой частоты. Для облегчения зацепления зубчатых колес при включении посредством перемещения по валу торцы зубьев со стороны включения закругляют.
Зубчатые передачи бывают открытые и закрытые. Открытые передачи тихоходные. Они не имеют корпуса и периодически смазываются густой смазкой. Закрытые передачи заключены в корпуса. Зубчатые колеса закрытых передач смазываются или в масляной ванне, или струйкой под давлением. По быстроходности зубчатые передачи разделяют: весьма тихоходные ν<0,5, тихоходные 0,5<ν<3, среднескоростные 3<ν<15, скоростные 15<ν<40, высокоскоростные ν>40.
Дата добавления: 2015-07-18; просмотров: 1116;
