Тема 3 Зубчатые передачи
Основные термины и определения. Зубчатая передача – механизм, использующий зацепления, передающий или преобразующий движение с изменением угловых скоростей и моментов. Принцип действия зубчатой передачи основан на зацеплении пары зубчатых колес (рис.3.1).
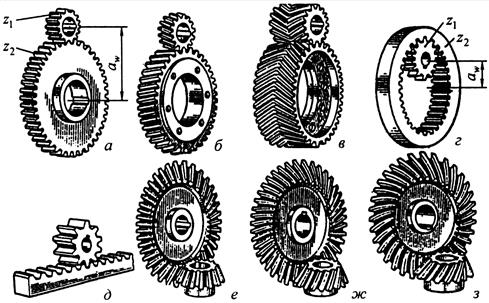
Рис. 3.1 Схема зубчатых передач
Зубчатые передачи, между параллельными валами осуществляются цилиндрическими колесами с прямыми, косыми и шевронными зубьями (рис.3.1,а-г) называют цилиндрическими. Существуют передачи (рис.3.1,а,б,в) внешнего зацепления и передачи (рис.3.1,г) внутреннего зацепления.. Передачи между валами с пересекающимися осями осуществляются коническими колесами с прямыми и круговыми зубьями (рис.3.1,е,з) реже тангенциальными зубьями (рис.3.1,ж). Зубчатые передачи для преобразования вращательного движения в поступательное осуществляют цилиндрическим колесом и рейкой (рис.3.1,д).
Для валов с перекрещивающимися осями применяют зубчато-винтовые, гипоидные и червячные передачи.

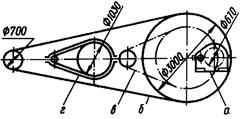 Оценка и применение. Зубчатые передачи обладают существенными достоинствами: малыми габаритами (рис.3.2); высоким КПД (до 0,97...0,98 в одной ступени); большой надежностью; постоянством передаточного отношения; возможностью применения в широком диапазоне моментов, скоростей и передаточных отношений.
Оценка и применение. Зубчатые передачи обладают существенными достоинствами: малыми габаритами (рис.3.2); высоким КПД (до 0,97...0,98 в одной ступени); большой надежностью; постоянством передаточного отношения; возможностью применения в широком диапазоне моментов, скоростей и передаточных отношений.
Для редукторов общего применения установлен ресурс ~30000 ч. К недостаткам зубчатых передач относят: требования высокой точности изготовления, шум при работе со значительными скоростями.
Наибольшее распространение получили передачи с цилиндрическими колесами. Зубчатая передача состоит из двух колес z1 и z2, расположенных на валах. Основными характеристиками передачи является мощности на валах Р1 и Р2 в кВт, угловые скорости ω1 и ω2 в с-1 (или частоты вращения n1 и n2 в мин-1), окружная скорость на делительном цилиндре ν в м/с, вращающие моменты Т1 и Т2 в Н·м, передаточное отношение и, коэффициент полезного действия η. При расчете передачи используются зависимости, известные из теоретической механики: и=ω1/ω2=n1/n2; ω=πn/30; ν=πdn/60000=ωd/2; Т1=1000Р1/ω1≈9550 Р1/n1; Р2=Р1/η; Т2=9550Р2/n2=Т1иη.
Стандартами установлены термины, определения и обозначения, относящиеся к геометрии и кинематике зубчатых передач, а также методы расчета геометрических параметров.
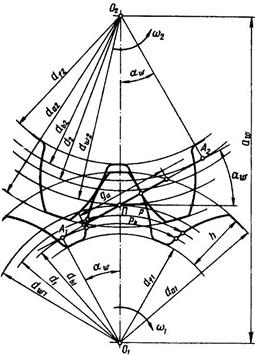 Основные параметры.Термин «зубчатое колесо» является общим. Зубчатое колесо с меньшим количеством зубьев из пары зубчатых колес называют шестерней, с большим числом зубьев — колесом. Параметрам шестерни приписывают индекс 1, а параметрам колеса—2 (рис.3.3). Различают индексы, относящиеся: w—к начальной поверхности или окружности; b—к основной поверхности или окружности; а—к поверхности или окружности вершин и головок зубьев; f—к поверхности или окружности впадин и ножек зубьев. Параметрам, относящимся к делительной поверхности или окружности, дополнительного индекса не приписывают.
Основные параметры.Термин «зубчатое колесо» является общим. Зубчатое колесо с меньшим количеством зубьев из пары зубчатых колес называют шестерней, с большим числом зубьев — колесом. Параметрам шестерни приписывают индекс 1, а параметрам колеса—2 (рис.3.3). Различают индексы, относящиеся: w—к начальной поверхности или окружности; b—к основной поверхности или окружности; а—к поверхности или окружности вершин и головок зубьев; f—к поверхности или окружности впадин и ножек зубьев. Параметрам, относящимся к делительной поверхности или окружности, дополнительного индекса не приписывают.
 Параметры пары зубчатых колес и их взаимосвязи рассмотрим для прямозубых колес: z1 и z2—число зубьев шестерни и колеса; р—делительный окружной шаг зубьев; pb=pcosα — основной окружной шаг зубьев; α—угол профиля делительный, по ГОСТ 13755—81, α=20°; αw—угол зацепления или угол профиля начальный:
Параметры пары зубчатых колес и их взаимосвязи рассмотрим для прямозубых колес: z1 и z2—число зубьев шестерни и колеса; р—делительный окружной шаг зубьев; pb=pcosα — основной окружной шаг зубьев; α—угол профиля делительный, по ГОСТ 13755—81, α=20°; αw—угол зацепления или угол профиля начальный:
cos αw=dcos α/dw
Основная характеристика размеров зубьев m=p/π — окружной модуль зубьев.
Значения модулей определены ГОСТ9563 — 60 в диапазоне 0,05...100 мм (табл.3.1).
Таблица 3.1 Значения модулей стандартизованных ГОСТ 9563 — 60
| Ряды | Модуль, мм |
| 1-й | 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25 |
| 2-й | 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22 |
d=pz/π — делительный диаметр; db=dcosα — основной диаметр (диаметр окружности, разверткой которой являются эвольвенты зубьев); dw1―начальные диаметры (диаметры окружностей, по которым пара зубчатых колес обкатывается в процессе вращения):
dwl=2αw/(z2/z1+l); dw2=2αw-dw1.
У передач без смещения и при суммарном смещении хΣ=0 начальные и делительные окружности совпадают:
dwl=d1=mz1; dw2=d2=mz2.
При нарезании колес со смещением делительная плоскость рейки смещается к центру или от центра заготовки на хт; х—коэффициент смещения исходного контура. Смещение от центра считают положительным (х>0), а к центру—отрицательным (х<0).
αw=0,5(dwl+dw2)—межосевое расстояние;
αw=m(0,5zΣ+xΣ-∆y),
где zΣ=z1+z2; xΣ=xl+x2; ∆у— коэффициент уравнительного смещения при xΣ≠0 (определяется по ГОСТ 16532—70). Для передач без смещения и при x1=—x2 или хΣ=0 ∆y=0 αw=a=0,5m(z1+z2), h=m(2 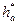 +c*-∆y) — высота зуба; da=d+2m(
+c*-∆y) — высота зуба; da=d+2m( 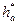 +x-∆y)—диаметр вершин зубьев; df=d—2m(
+x-∆y)—диаметр вершин зубьев; df=d—2m( 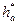 +c*—x) — диаметр впадин;
+c*—x) — диаметр впадин; 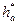 — коэффициент высоты головки зуба (по ГОСТ 13755—81,
— коэффициент высоты головки зуба (по ГОСТ 13755—81, 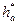 =1); с*—коэффициент радиального зазора (по ГОСТ 13755—81, с*=0,25).
=1); с*—коэффициент радиального зазора (по ГОСТ 13755—81, с*=0,25).
Для колес без смещения h=2,25m; dа=d+2m; df=d—2,5m; А1А2—линия зацепления (общая касательная к основным окружностям); gа—длина активной линии зацепления; П—полюс зацепления точка пересечения линии центров колес 0102 с линией зацепления.
Расчет основных геометрических и кинематических параметров представлен в табл.3.2.
Дата добавления: 2015-07-18; просмотров: 1382;
