Угловая скорость и угловое ускорение

Любое движение точки можно разложить на поступательное движение (скорость не меняет своего направления) и вращение по окружности.

Любое движение твердого тела можно свести к поступательному движению центра масс этого тела и вращению. При вращении тела его разные точки проходят разные пути за время одного оборота, поэтому скорости разных точек различны. Имеется, однако, величина, которая характеризует вращение всех точек тела. Это угол вращения φ. Он измеряется в радианах (напомним, что 1 рад - угол, который стягивает дугу, равную радиусу, 1 рад»57°).

При вращении твердого тела угловая скорость 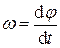одинакова для всех точек тела. Угловая скорость измеряется в рад/с или 1/с (в размерности радианы обычно не пишут). Линейная скорость V точки, находящейся на расстоянии r от оси вращения, равна V = ωr. Эту формулу легко запомнить, если учесть, что размерности справа и слева должны совпадать.

Угловое ускорение 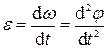измеряется в 1/с².

Кинетическая энергия вращающегося твердого тела

Найдем кинетическую энергию вращающегося тела, считая, что это тело состоит из отдельных точек, каждая массой т_i:

.

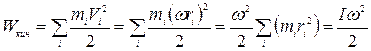Величину I называют моментом инерции твердого тела.

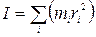. (4.2)

Момент инерции измеряют в кг·м². При поступательном движении инертность тела характеризуется его массой. Момент инерции характеризует инертность тела при его вращении. Величина I зависит от массы (распределения масс т_i), формы тела и положения оси вращения. Для одного и того же тела момент инерции может оказаться совершенно разным, если оси вращения различны. Например, стержень массой т и длиной l имеет момент I₁ = 1/12тl², если ось вращения проходит через его середину, и момент I₂= 1/Зтl², если ось вращения находится на конце стержня. Для диска I = 1/2mR², для шара I = 2/5тR².

З а д а н и е: 1) рассчитайте момент инерции трех точек массой т на спице длиной l (рис. 4.1). Попытайтесь угадать сразу, в каком случае момент инерции будет больше.

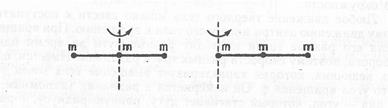
Рис. 4.1. К определению момента инерции тела

относительно различных осей вращения

2) Рассчитайте, как изменится момент инерции трех точек массой m на спице, если спицу согнуть, как показано на рис. 4.2.

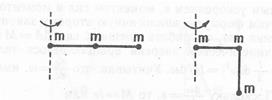
Рис. 4.2. К определению момента инерции

трех точек одинаковой массы

Работа при вращении твердого тела

Найдем работу, которую необходимо затратить, чтобы повернуть твердое тело на угол dφ.

При вращении на малый угол dφ точка проходит путь r dφ (r - расстояние точки до оси вращения). Если вращение происходит под действием силы F, то работа этой силы равна

dA = Fr dφ cos α = Fl dφ = М dφ. (4.3)

Величину l = rcosα называют плечом силы. Плечо — это кратчайшее расстояние от оси до направления действия силы (рис. 4.3). Произведение силы на плечо носит название момента силы M = Fl.

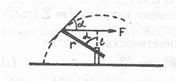
Рис. 4.3. Нахождение момента силы

Чтобы увеличить момент силы, можно увеличить приложенную силу F или удлинить плечо l. Поэтому дверные ручки делают подальше от оси вращения двери, а гаечные ключи делают длинными.

Рассмотрим, в каких случаях момент силы становится равен нулю. Очевидно, это происходит, когда направление действия силы проходит через ось вращения и l=0. Таким образом, не всякая сила способна создать момент и привести тело во вращение.

Во п р о с ы: почему длинную палку легче удержать в горизонтальном положении, взяв ее за середину, а не за конец? Почему целую спичку легче переломить, чем ее половинки? Чему равен момент силы, действующий на электрон, вращающийся по орбите (рис. 1.3). Чему равен момент инерции вращающегося электрона?

Основной закон динамики вращательного движения

При вращательном движении силовой характеристикой является момент силы М, а инерционные характеристики вращающегося тела определяются моментом инерции I. Установим связь между угловым ускорением ε, моментом сил и моментом инерции, то есть получим формулу, аналогичную второму закону Ньютона.

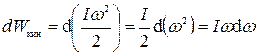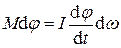Если трения нет, то работа внешних сил dA=Mdφ идет на увеличение кинетической энергии вращающегося тела . Учитывая, что , имеем . Поскольку 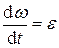, то М = Iε или

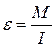. (4.4)

Угловое ускорение твердого тела пропорционально моменту силы и обратно пропорционально моменту инерции. Это основной закон динамики вращающегося тела.

Ниже сопоставим характеристики тела при поступательном и вращательном движениях.

Поступательное движение: Вращательное движение:

смещение х (м), угол поворота (смещение) φ (рад),

скорость V = dx/dt (м/с), угловая скорость ω = dφ/dt (1/с),

ускорение a=d²x/dt² (м/с²), угловое ускорение ε = d²φ/dt² (1/с²).

масса 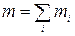(кг), момент инерции 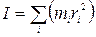(кг·м²),

кинетическая энергия кинетическая энергия

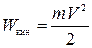(Дж), (Дж),

сила F (Н), момент силы M=Fl (Н·м),

уравнение Ньютона уравнение динамики вращающегося

а = F/m, тела ε = М/I,

импульс (количество движения) момент импульса (момент

P=mV (кг·м/с), количества движения) L=mVr

(кг·м²/с),

закон сохранения импульса в закон сохранения момента

отсутствии внешних сил. импульса в отсутствии сил

вращения.

Физический маятник

Если на нити качается материальная точка, то это математический маятник. Если же на нити качается тело или несколько материальных точек, то это физический маятник. Рассмотрим, как зависит период колебания Т физического маятника от расстояния х между точками на нити.

Пусть на нити длиной l имеются две материальные точки одинаковой массы т, расположенные на расстоянии х друг от друга (рис. 4.4).

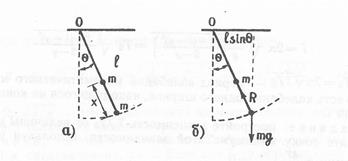
Рис. 4.4. Физический маятник из двух одинаковых масс на нити (а)

и силы, действующие на груз (б)

Как известно, на груз, подвешенный на нити, действует сила тяжести F_гр=mg, направленная вертикально вниз, и сила реакции опоры R, направленная вдоль нити. Очевидно, вращающий момент создает только сила F_гp. Плечо этой силы равно lsin θ, и, следовательно, момент силы М₁ = mgl sin θ. Аналогично находится момент силы M₂ = mg(l-x)sinθ, действующий на вторую массу. Суммарный момент равен

М = М₁ + М₂ = mg(2l-х) sinθ. (4.5)

Момент инерции двух масс на нити равен

I = тl²+т(l-х)². (4.6)

Согласно основному уравнению динамики 4.4 имеем

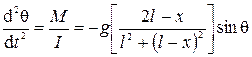. (4.7)

В формуле (4.7) стоит знак минус, поскольку момент сил стремится уменьшить угол θ, возвращая систему к положению равновесия. Если отклонения нити от положения равновесия невелики, θ«1 (угол θ измеряется в радианах, 1 рад»57°), то sinθ»θ и уравнение 4.7 приобретает вид:

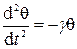, (4.8)

где 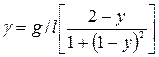, y=x/l.

Дифференциальное уравнение движения 4.8 описывает гармонические колебания с частотой 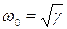(формулы 3.2, 3.3) и периодом 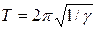. Таким образом, период колебаний физического маятника (двух шариков на нити) равен

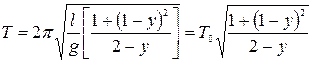, (4.9)

где 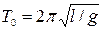- период колебаний математического маятника, то есть колебаний одного шарика, находящегося на конце нити длиной l.

З а д а н и е: постройте зависимость Т/Т₀ от величины у=х/l. Найдите точку минимума этой зависимости, используя условие экстремума .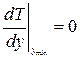

Оборотный маятник

Если один из грузов на стержне маятника находится выше оси вращения, то такой маятник называется оборотным (рис. 4.5).

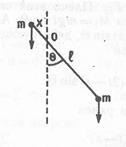
Рис. 4.5. Оборотный маятник

Из рис. 4.5 ясно, что результирующий момент сил в оборотном маятнике равен

M = mgl sin θ - mgx sin θ, (4.10)

а момент инерции

I = ml² + mx². (4.11)

Подставляя (4.10), (4.11) в основное уравнение динамики, имеем

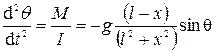. (4.12)

При малых углах (θ«1) можно считать, что sinθ»θ, и записать дифференциальное уравнение движения 4.12 в виде

, (4.13)

где , .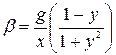

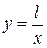Период колебаний оборотного маятника равен

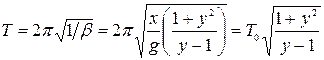, (4.14)

где 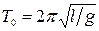— период колебаний математического маятника, состоящего только из нижнего груза.

З а д а н и е: постройте зависимость Т/Т₀ от у=l/х. Заметим, что y< 1 и, следовательно, х<l. Если х>1, то есть верхний груз |расположен от оси вращения дальше, чем нижний, то маятник перевернется. Когда плечо верхнего груза х приближается к l, то есть при (l—х)/l«1, период колебаний стремится к бесконечности в соответствии с зависимостью t=T₀[l/(l - х)]^1/2.

Маятник Обербека

Для экспериментального определения моментов инерции вращающихся твердых тел используют Маятник Обербека. Он представляет собой диск с четырьмя стержнями, на которые надеты цилиндры. Цилиндры можно смещать по стержням, изменяя их расстояние от оси О (рис. 4.6).

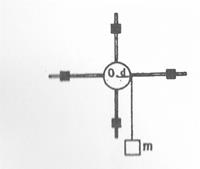
Рис 4.6. Маятник Обербека

На диск намотан шнур, к концу которого можно подвешивать груз массой m. Груз создает силу натяжения F_н = m(g - a), где а - ускорение, с которым движется вниз этот груз. Момент этой силы M = F_нd. Под действием момента силы маятник раскручивается с угловым ускорением ε = М/I = F_нd/I = m(g-a)d/I. Поскольку угловое ускорение ε связано с ускорением движения груза соотношением εd=а, то из уравнения a/d = m(g-a)d/I находим I = md²(g/a-1). Измерив ускорение а, по этой формуле определяют момент инерции I.

В о п р о с ы: 1) как зависит момент инерции маятника Обербека I от массы груза т? 2) как зависит момент инерции маятника от величины плеча d? 3) от чего зависит угловое ускорение ε маятника Обербека? 4) что нужно сделать, чтобы ε увеличилось?

ЛИТЕРАТУРА

1. Лаврова И. В. Курс физики: Учебн. пособие для студентов биолог.-хим. факультетов мед. институтов. М.: Просвещение 1981. 256 с: ил.

2 Зисман Г. А., Тодес О. М. Курс общей физики. В 3 т. Т 1. М.: Наука, 1974, 340 с: ил.

3. Детлаф А. А., Яворский Б. М., Милковская Л. Б. Kурс физики. В 3 т. Т. 1. М.: Высш. шк., 1977. 411 с: ил.

Составители:

А. М. Скворцов, И.В. Павлушков,

Е. Д. Эйдельман,