КИНЕМАТИКА. Задача кинематики состоит в изучении зависимости смещения тела х от времени движения t.

Задача кинематики состоит в изучении зависимости смещения тела х от времени движения t.

Поскольку скорость есть первая производная от смещения по времени 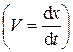, а ускорение — вторая производная 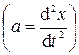, то зная зависимость x(t), легко найти V(t) и a(t).

Чтобы найти зависимость x(t), обычно приходится решать дифференциальное уравнение движения, то есть использовать второй закон Ньютона: 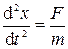. Рассмотрим несколько конкретных случаев.

Движение в отсутствии сил. В случае движения в отсутствии сил ускорение равно нулю (а = 0), и, следовательно, скорость постоянна (V=V₀), а смещение линейно зависит от времени, x(t)=x₀+ V₀t.

Движение под действием постоянной силы. Пусть на тело действует постоянная сила F₀. Тогда дифференциальное уравнение движения имеет вид: d²х/dt² = F₀/m. Его решением является зависимость

, (3.1)

где а = F₀/m.

З а д а н и е: постройте зависимость скорости и смещения от времени при равноускоренном (a>0) и равнозамедленном (а<0) движениях.

Движение под действием силы упругости. По закону Гука внутренняя сила пропорциональна смещению: F_yпp= - kx. Поэтому дифференциальное уравнение движения имеет вид:

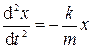. (3.2)

Решение этого уравнения ищут в виде x(t) = A cos (ω₀t+φ), где ω₀ - некоторая, пока еще неизвестная, частота колебаний тела.| IIодставив предполагаемое решение в уравнение 3.2, получаем, что 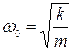, и, следовательно, зависимость смещения от времени имеет вид гармонического колебания:

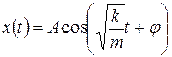. (3.3)

Период колебания 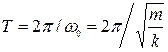зависит от массы тела m и коэффициента жесткости k. Амплитуда А и начальная фаза φ колебаний определяются начальными условиями.

З а д а н и е: получите формулы для скорости и ускорения движения под действием внутренней упругой силы.

Движение под действием внешней периодической силы при наличии силы упругости. Пусть тело массой m прикреплено к пружине, и на тело действует внешняя периодическая сила F_вн=F₀cos(ωt), где F₀— максимальная величина силы, а ω — частота действия силы. Тогда тело будет совершать вынужденные колебания. Результирующая сила складывается из двух сил: внутренней силы упругости пружины F_вн= -kx и внешней периодической силы F_вн ~ cos (ωt). Дифференциальное уравнение движения имеет вид:

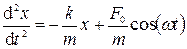. (3.4)

Смещение x(t) определяют по уравнению

x(t)=A(ω)cos(ωt)/ (3.5)

Подставляя (3.5) в (3.4), получим

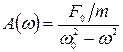, (3.6)

где .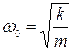

Итак, под действием внешней периодической силы тело колеблется с той же частотой ω (с тем же периодом), что и сила. При этом амплитуда колебания зависит от соотношения собственной частоты колебания ω₀ и частоты внешней силы ω и при ω»ω₀ становится бесконечно большой.

З а д а н и е: постройте зависимость амплитуды колебаний А от частоты внешней силы ω.

Движение при наличии силы вязкого трения. Пусть на тело, двигающееся по инерции со скоростью V₀, начинает действовать сила вязкого трения F_тр=-fV. Напомним, что f – коэффициент трения, зависящий от вязкости среды η, и размеров тела R (для шарообразных тел f=6πηR)Напишем дифференциальное уравнение движения:

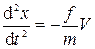(3.7)

или

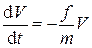. (3.8)

Разделим переменные и проинтегрируем уравнение (при t=0, V=V₀):

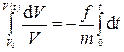, (3.9)

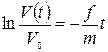, (3.10)

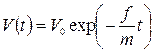. (3.11)

Итак, под действием сил трения скорость тела уменьшается экспоненциально в течение времени.

Теперь найдем зависимость смещения (пути тела) от времени, то есть x(t), считая, что в начальный момент х(0) — 0:

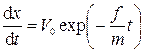, (3.12)

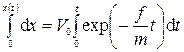, (3.13)

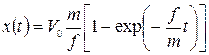. (3.14)

3 а д а н и е: нарисуйте зависимость скорости тела и его смещения от времени. В каких единицах измеряется величина f/т, какой физический смысл она имеет?

Движение тела, брошенного под углом к горизонту. Рассмотрим движение брошенного тела (рис. 1.1). На рис. 3.1 показана скорость тела в различных точках его траектории. Разложим эту скорость на две составляющие — вдоль горизонтальной оси х и по вертикальной оси у. Поскольку в горизонтальном направлении сил нет (рис. 1.1), то горизонтальная составляющая скорости

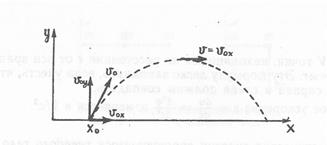
Рис. 3.1. Скорость тела, брошенного под углом к горизонту

всегда остается неизменной (V_0х), и, следовательно, в горизонтальном направлении тело движется равномерно: смещение х линейно меняется со временем, т. е. х(t) = х₀+ V_oxt. В то же время в вертикальном направлении действует постоянная сила (сила тяжести F_гр). Поэтому в вертикальном направлении тело движется с постоянным ускорением и 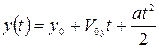. Ускорение, как и сила F_гр, всегда направлено вниз и равно а =-F_гр/m (знак минус показывает, что ускорение направлено против оси у). Если тело брошено с поверхности Земли, то у₀ = 0 и

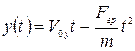. (3.15)

Нетрудно показать, что зависимость y(t) является параболой. Итак, движение брошенного тела складывается из линейного по времени смещения по горизонтали и квадратичного по времени смещения по вертикали.