Стоячая электромагнитная волна.

Мы уже говорили, что стоячую упругую волну можно представить как результат суперпозиции двух одинаковых волн, бегущих навстречу друг другу. Это относится и к элект­ромагнитным волнам. Однако надо учесть, что электромагнит­ная волна характеризуется не одним вектором, а двумя взаим­но ортогональными векторами 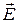и .

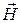Пусть волна распространяется в положительном направле­нии оси х и описывается уравнениями

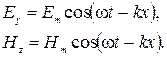(3.3.28)

Для волны, распространяющейся в обратном направлении, как мы знаем, в скобках мину­сы заменяются на плюсы. Кроме того, будем помнить, что векторы 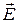, , 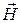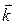должны составлять правую тройку.

Это поясняет рис.3.3.2, где в части (а) показаны возможные ориентации векторов 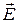и 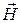в волне, распространяющейся в прямом, а в 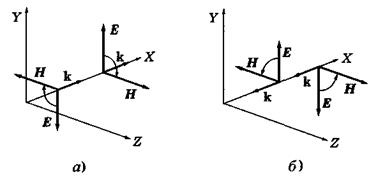части (б) – в обратном направлении. Рис.3.3.2.

Таким образом, при сложении волн

либо векторы 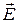, либо 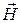будут иметь противоположные направления, а, значит, при векторном сложении их модули будут вычитаться. Итак, уравнения встречной вол­ны будут иметь вид:

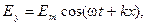
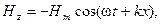(3.3.29)

или 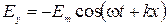, 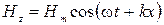. (3.3.30)

В результате суперпозиции двух встречных волн, (3.3.28) и (3.3.29), получим:

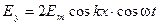
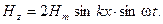(3.3.31)

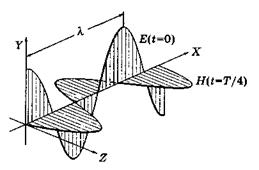Это и есть уравнения стоячей электромагнитной волны. Видно, что в этой волне колебания векторов 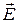и 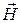сдвинуты по фазе на π/2 как в пространстве, так и во времени. Если в некоторый момент E_y во всех точках имело максимальное зна­чение и при этом H_z = 0, то через четверть периода картина будет обратной: H_z достигнет всюду максимальных значений со сдвигом в пространстве на λ/4, а E_y обратится в нуль. Таким образом, в процессе колебаний электрическое поле посте­пенно переходит в магнитное, магнитное — в электрическое Рис.3.3.3.

и т. д. (см. рис.3.3.3). Поскольку колебания векторов 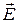и 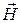происхо­дят не в фазе, соотношение (3.3.13) оказывается справедливым только для амплитудных значений Ε_m и Η_m стоячей волны:

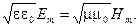(3.3.32)

В стоячей электромагнитной волне энергия переходит из чис­то электрической, имеющей максимумы в пучностях 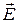, в маг­нитную с максимумами в пучностях вектора 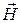, т. е. смещенным в пространстве на λ/4. Таким образом, происходит преобразование энергии электрического поля в энергию мгнитного и наоборот на расстоянии четверти длины волны. Это аналогично поведению гармоническо­го осциллятора, например математического маятника, где энер­гия переходит из чисто потенциальной (в крайнем положении) в кинетическую (в положении равновесия), и наоборот. Макроскопического переноса энергии не происходит. Отсюда и название волны – стоячая.

Электромагнитная волна на границе раздела диэлектриков

Выясним, что происходит при падении плоской электромагнитной волны на границу раздела двух однородных изотропных прозрачных диэлектриков, магнитная проницаемость которых равна единице (µ = 1). Известно, что при этом возникают отраженная и преломленная волны. Ограничимся рассмотрением частного, но практически важного случая, когда волна падает нормально на границу раздела диэлектриков с показателями преломления n₁ и n₂.

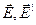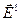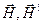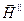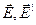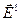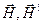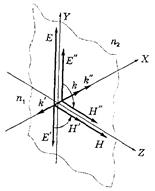
Обозначим электрическую составляющую в падающей, отраженной и преломленной волнах соответственно через и , а магнитную составляющую — через и . Из соображений симметрии ясно, что колебания векторов и происходят в одной плоскости. Это же относится и к векторам и 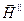. На рисунке показаны относительное расположение этих векторов в непосредственной близости от границы раздела и направления распространения всех трех волн, обозначенные векторам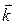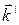и , и 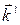. Дальнейший расчет покажет, насколько эта картина соответствует действительности.

Воспользуемся граничными условиями для

тангенциальных составляющих векторов 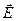и 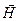: Рис.3.3.4.

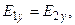
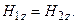(3.3.33)

Перепишем эти условия для нашего случая:

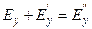(3.3.34)

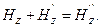(3.3.35)

Согласно (3.3.14),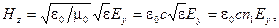

Тогда 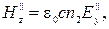но 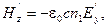поскольку проекции E’_y и Н’_z, в отраженной волне имеют противоположные знаки (см. рис.3.3.4). Поэтому равенство (3.3.35) можно переписать так: 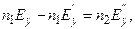или

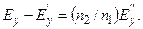(3.3.36)

Решив совместно уравнения (3.3.34) и (3.3.36), получим выражения для Е’_y и Е”_y через Е_y, которые в векторной форме имеют вид:

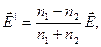
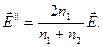(3.3.37)

Отсюда следует, что:

1. Вектор 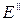всегда сонаправлен с вектором 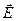, т. е. оба вектора колеблются синфазно — при прохождении волны через границу раздела фаза не претерпевает скачка.

2. Это же относится и к векторам 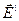и 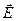, но при условии, что n₁ > n₂, т. е. если волна переходит в оптически менее плотную среду. В случае же, когда n₁ < n₂, дробь в выражении (3.3.37) для 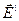оказывается отрицательной, а это означает, что направление вектора 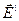противоположно направлению вектора 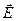, т. е. колебания этих векторов происходят в противофазе (этому соответствует рис.3.3.4). Другими словами, при отражении волны от оптически более плотной среды фаза колебаний вектора 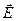изменяется скачком на π.

Эти результаты мы будем использовать в дальнейшем при изучении интерференции волн, отраженных от поверхностей тонких пластинок.

Коэффициенты отражения и пропускания.

Вопрос об этих коэффициентах мы рассмотрим для случая нормального падения световой волны на границу раздела двух прозрачных диэлектриков. Ранее мы выяснили, что интенсивность I гармонической волны, пропорциональна 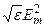. Коэффициент отражения, по определению, есть 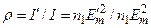. После подстановки отношения Е’_m /Е_m из первой формулы (3.3.37), найдем:

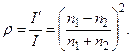(3.3.38)

Обратим внимание на то, что r не зависит от направления падающей волны на границу раздела: из среды 1 в среду 2, или наоборот. При небольшой разнице показателей преломления граничащих сред этот коэффициент оказывается очень небольшим (на границе стекло – воздух он составляет 0,04)

Аналогично находим и коэффициент пропускания t как отношение I’’/I. Согласно (3.3.27), I”/I = 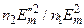. Остается учесть вторую формулу из (3.3.37), и мы получим, что коэффициент пропускания

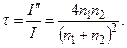(3.3.39)

Нетрудно убедиться в том, что сумма обоих коэффициентов r + t = 1, как и должно быть.