Поляризация волн. Поляризация света. Способы поляризации.

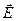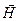Как уже указывалось,электромагнитная волна является поперечной. Это значит, что векторы и всегда лежат в плоскости перпендикулярной направлению распространения волны (лучу). Однако, как именно в этой плоскости расположены эти векторы, зависит от источника волны. (В дальнейшем будем вести речь о световом векторе )

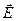В зависимости от длины волны (или частоты) различают несколько видов электромагнитных волн: радиоволны, оптический диапазон, рентгеновское и гамма-излучения. В дальнейшем нас будет интересовать главным образом оптический диапазон длин волн. Его подразделяют на

инфракрасное излучение ………..l ~ 1 мм ÷ 0,76 мкм,

видимое излучение (свет) ……….l ~ 0,76 ÷ 0,40 мкм,

ультрафиолетовое излучение...... .l ~ 0,40 ÷ 0,01 мкм.

Соответствующие длины волн указаны в вакууме.

По классическим представлениям излучение светящегося тела (газа) слагается из волн, испускаемых его атомами. Излучение отдельного атома продолжается порядка 10^-8 c и представляет собой, как говорят, цуг волн. Излучив, атом через некоторое время, придя в возбужденное состояние, излучает опять и т. д. Одновременно излучает множество атомов. Порожденные ими цуги волн, налагаясь друг на друга, образуют испускаемую телом световую волну. Направления колебаний для каждого цуга ориентированы случайным образом. Поэтому в результирующей световой волне колебания светового вектора происходят в разных направлениях с равной вероятностью, оставаясь в плоскости перпендикулярной лучу. Это надо понимать так, что при прохождении световой волны через некоторую точку колебания светового вектора быстро и беспорядочно сменяют друг друга. Такой свет называют неполяризованным или естественным.

Существуют способы упорядочивания колебаний световой волны. Свет, в котором направление колебаний светового вектора упорядочено каким-либо образом, называют поляризованным. Если колебания светового вектора происходят только в одной плоскости, содержащей луч и вектор 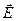свет называют плоско- (или линейно-) поляризованным (конец вектора 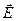описывает прямую линию в плоскости перпендикулярной лучу. В этом случае вектор 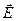меняется только по величине, не меняя направления. Плоскость, в которой происходят колебания светового вектора, называют плоскостью поляризации волны.

Если конец светового вектора описывает в этой плоскости эллипс, то такой свет называют эллиптически-поляризованным. Частным случаем такой поляризации является круговая или циркулярная, когда световой вектор меняется только по направлению, не меняясь по модулю. В зависимости от направления вращения вектора 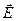различают правую и левую эллиптические (или круговые) поляризации. Если смотреть навстречу распространения волны, и вектор 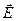при этом поворачивается по часовой стрелке, то поляризацию называют правой, в противном случае (если против часовой стрелки) — левой.

Создание принципиально нового источника света — лазера позволило получить плоско-поляризованный свет с высокой степенью монохроматичности. Использование такого источника света сильно упростило экспериментальное решение многих вопросов, связанных с интерференцией, дифракцией и др.

Способы поляризации света.

1. Поляризация при отражении света на границе раздела диэлектриков.

Естественный свет можно представить как наложение (сумму) двух некогерентных (несогласованных) плоскополяризованных волн с взаимно ортогональными плоскостями поляризации.

Рассматривая отражение и преломление волны, падающей под произвольным углом на границу раздела диэлектриков, можно найти соотношения между амплитудами и фазами падающей, отраженной и преломленной волн – так называемые формулы Френеля. При необходимости с ними можно познакомиться во многих учебниках и справочниках.

Мы не будем выписывать эти формулы, поскольку для решения наших вопросов они нам не понадобятся. Важно отметить только, что с помощью этих формул можно показать, что при произвольном угле падения 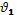(и соответствующем ему угле преломления 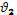) коэффициенты отражения линейно-поляризованного света, плоскость поляризации которого перпендикулярна плоскости падения ( 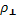) и параллельна ей ( 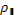), определяются следующими выражениями:

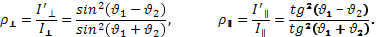(3.4.1)

Поскольку эти коэффициенты различны то отраженный и преломленный пучки оказываются частично-поляризованными. В отраженном свете преобладают колебания вектора , перпендикулярные к плоскости падения, а в преломленном свете, параллельные плоскости падения. Степень поляризации обеих волн (отраженной и преломленной) зависит от угла падения. Рис.3.4.1.

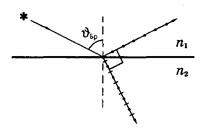
При некотором значении угла падения отраженный

свет становится полностью поляризованным, и его плоскость поляризации (плоскость колебаний вектора ) оказывается перпендикулярной к плоскости падения. Такое явление наблюдается, когда 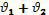= p/2, т.е. отраженный и преломленный лучи ортогональны, и значит, tg(p/2)=∞ .Тогда коэффициент отражения 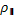= 0, т. е. отраженный свет будет полностью линейно-поляризованным в плоскости, перпендикулярной плоскости падения. Угол падения, при котором наблюдается такой эффект называется углом Брюстера или углом полной поляризации. Этот угол 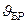удовлетворяет следующему условию:

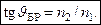(3.4.2)

На рис.3.4.1. представлена именно такая ситуация. Точками и черточками на отраженном и преломленном лучах этого рисунка показаны направления колебаний вектора .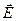

2. Поляризация при двойном лучепреломлении.

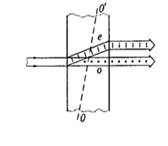Почти все прозрачные кристаллические диэлектрики оптически анизотропны, т. е. оптические свойства света при прохождении через них зависят от направления. Вследствие этого возникает явление, называемое двойным лучепреломлением. Оно заключается в том, что падающий на кристалл пучок света разделяется внутри кристалла на два пучка, распространяющиеся, вообще говоря, с разными скоростями.

Существуют кристаллы одноосные и двуосные. У одноосных кристаллов один из преломленных пучков подчиняется обычному закону преломления ( 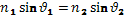). Его называют обыкновенным и обозначают буквой или индексом о. Другой пучок необыкновенный (e), он не подчиняется обычному закону преломления, и даже при нормальном падении светового Рис3.4.2.

пучка на поверхность кристалла необыкновенный пучок может

отклоняться от нормали (рис.3.4.2). И, как правило, необыкновенный луч не лежит в плоскости падения.

Наиболее сильно двойное лучепреломление выражено у таких одноосных кристаллов как кварц (кристаллический), исландский шпат и турмалин.

Далее мы ограничимся рассмотрением только одноосных кристаллов. У одноосных кристаллов имеется направление – оптическая ось 00’ - , вдоль которого обыкновенная и необыкновенная волны распространяются, не разделяясь пространственно и с одинаковой скоростью (у двуосных кристаллов, например слюды, имеются два таких направления).

Оптическая ось 00’ кристалла не является какой-то особой прямой линией. Она характеризует лишь избранное направление в кристалле и может быть проведена через произвольную точку кристалла.

Любую плоскость, проходящую через оптическую ось, называют главнымсечением или главной плоскостью кристалла. Обычно пользуются главным сечением (плоскостью), проходящим через световой луч в кристалле.

Обыкновенная и необыкновенная волны (и лучи) линейно поляризованы. Колебания вектора 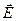в обыкновенной волне совершаются в направлении, перпендикулярном главному сечению кристалла для обыкновенного луча. Колебания же вектора 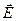в необыкновенной волне – в главном сечении кристалла обыкновенного луча. Направления колебаний вектора 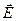(т.е. их плоскости поляризации) в обоих пучках показаны на рис.3.4.2, где предполагается, что оба пучка и пересекающая их оптическая ось 00’ лежат в плоскости рисунка. Видно, что в данном случае плоскости поляризации обеих волн (о и е) взаимно ортогональны. Заметим, что это наблюдается практически при любой ориентации оптической оси, поскольку угол между обыкновенным и необыкновенным лучами достаточно мал.

Оба луча, вышедшие из кристалла, отличаются друг от друга только направлением поляризации, так что названия «обыкновенный» (о) и «необыкновенный» (е) имеют смысл только внутри кристалла.

Раздвоение световых лучей обусловлено зависимостью показателя преломления среды от направления светового вектора волны. Световую волну, падающую на кристалл, можно представить как совокупность двух линейно поляризованных волн, у одной из которых плоскость поляризации перпендикулярна главному сечению кристалла (обыкновенный луч), а у другой – параллельна ему (необыкновенный луч). Скорость распространения обыкновенной волны и, следовательно, показатель преломления для нее 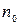не зависят от направления распространения (т.е. эта волна ведет себя в кристалле как в изотропной среде). Скорость же распространения и показатель преломления необыкновенной волны 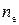зависят от направления распространения. Таким образом, законы преломления для необыкновенного луча изменяются, в частности, он может не лежать в плоскости падения. При распространении вдоль оптической оси оба показателя преломления совпадают, поэтому раздвоения луча не происходит. Наибольшее отличие 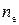от 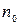наблюдается при распространении в направлении перпендикулярном оптической оси.

Поляризаторы. Закон Малюса.

Устройства, с помощью которых можно получить из естественного поляризованный свет (обычно линейно-поляризованный) называются поляризаторами. Действие таких приборов может быть основано на двух вышеназванных явлениях. В любом случае вышедший из поляризатора свет линейно поляризован, а плоскость, проведенная через вектор 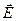и вышедший луч, называется плоскостью поляризатора. Поляризатор пропускает лишь волну, колебания вектора 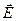в которой параллельны этой плоскости.

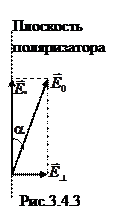Пусть на поляризатор падает плоско-поляризованная волна. Плоскость, проведенная через вектор 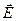и луч, называется плоскостью поляризации. Пусть плоскость поляризации падающей волны составляет с плоскостью поляризатора угол 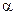. Такую волну можно представить как суперпозицию двух других, у одной из которых плоскость поляризации параллельна плоскости поляризатора, а у другой – перпендикулярна (рис.3.4.3). Поляризатор пропустит лишь первую из них. Из рисунка видно, что 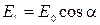. А поскольку интенсивность волны пропорциональна квадрату амплитуды, то интенсивность вышедшей из поляризатора волны I связана с интенсивностью падающей I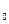

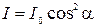. (3.4.3)

Соотношение (3.4.3) называется законом Малюса. Если падающий свет естественный, то угол 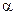хаотически меняется в пределах от 0 до 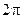и при усреднении соотношения (3.4.3)получим интенсивность вышедшего луча

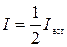. (3.4.4)