Фазовая и групповая скорости волны. Дисперсия.

В вакууме все электромагнитные волны распространяются с одинаковой скоростью, называемой скоростью света - с. Скорость же распространения волн разных частот в веществе будет различной. Дело в том, что электрические диполи диэлектрика под влиянием электромагнитного поля волны совершают вынужденные колебания. Электромагнитное излучение, вызванное колебаниями этих диполей, создает вторичную волну, которая, накладывается на исходную (первичную) и дает результирующую волну в веществе. Это наложение оказывается достаточно сложным и в результате скорость волны оказывается зависящей от ее частоты.

Строго монохроматическая волна представляет собой бесконечную во времени и пространстве последовательность «горбов» и «впадин», перемещающихся вдоль оси х с фазовой скоростью

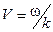. (3.5.1)

С помощью такой волны нельзя передать никакого сигнала, так как каждый последующий «горб» или «впадина» ничем не отличаются от предыдущего.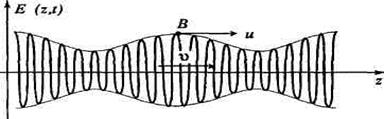

Рис.3.5.1.

Однако, как уже отмечалось, монохроматическая волна это идеализация. Реально любая волна представляет собой некую совокупность (суперпозицию) волн с частотами, заключенными в некотором интервале 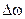. Если этот интервал невелик, то такая совокупность называется волновым пакетом или группой волн. С помощью такой системы можно передавать сигнал (рис.3.5.1)

Рассмотрим простейший случай. Пусть волновой пакет состоит из двух волн с одинаковыми амплитудами и небольшим отличием по частотам (а следовательно и по волновым числам)

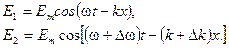, (3.5.2)

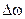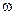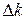где « и «k. Тогда, сложив эти две волны, получим

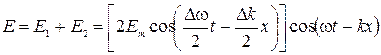. (3.5.3)

Выражение, стоящее в квадратных скобках, можно считать амплитудой волнового пакета (огибающая на рис.3.5.1). Эта амплитуда меняется в пространстве и во времени, но фиксировав некоторое ее значение, например максимум (точка В на рисунке) можно передавать информацию.

Найдем скорость этой точки. Для этого фиксируем некоторое значение амплитуды. За время dt это значение переместится на dx . Тогда можно записать

,

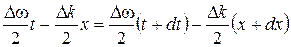Откуда получим

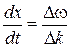. (3.5.4)

Эта величина есть не что иное, как скорость перемещения амплитуды волнового пакета, называемая групповой скоростью. Это также скорость перемещения энергии. Мы получили это выражение для группы, состоящей из двух волн. В общем случае для групповой скорости, которую обозначим u, имеет место выражение

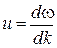. (3.5.5)

Напомним, что фазовая скорость волны 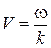. (3.5.6)

Найдем связь между групповой и фазовой скоростью. Учтем связь между длиной волны и волновым числом 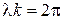. Тогда получим

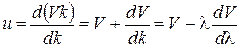. (3.5.7)

Из полученного соотношения следует, что, если фазовая скорость не зависит от частоты (или длины волны), то групповая и фазовая скорости одинаковы и форма волнового пакета не меняется. Если же фазовые скорости для разных составляющих пакета различны, то V ≠ u и форма волнового пакета меняется (пакет расплывается).

Явление зависимости фазовой скорости (а, следовательно, и показателя преломления вещества) от длины волны (или частоты) называется дисперсией.

Дисперсия света.

Дисперсия света объясняется зависимостью диэлектрической проницаемости 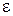, а, следовательно, и показателя преломления от частоты (или длины волны ). Эта зависимость связана с взаимодействием электромагнитного поля световой волны с атомами и молекулами, показатель преломления при этом становится комплексной величиной, содержащей действительную часть – истинный показатель преломления п и мнимую часть – коэффициент поглощения אּ. В видимой и ультрафиолетовой областях спектра основное значение имеют колебания электронов, а в инфракрасной - колебания ионов.
Согласно классическим представлениям, под действием электрического поля световой волны электроны атомов или молекул совершают вынужденные колебания с частотой, равной частоте приходящей волны 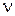. При приближении частоты световой волны к частоте собственных колебаний электронов 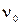возникает явление резонанса, обусловливающее поглощение света. Эта теория хорошо объясняет связь дисперсии света с полосами поглощения

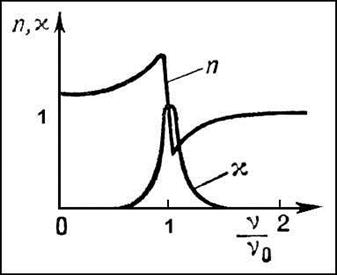
Рис.3.5.2.

На рис 3.5.2. показана зависимость показателя преломления и коэффициента поглощения от отношения частоты волны к собственной частоте электронов. Видно, что в области, где 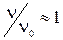, характер зависимости показателя преломления от частоты волны резко меняется и резко увеличивается коэффициент затухания. Область, где п растет с увеличением частоты, называется нормальной дисперсией, а , если п убывает с ростом частоты – аномальной дисперсией. Из графика видно, что аномальная дисперсия наблюдается при частотах, которые соответствуют сильному поглощению.

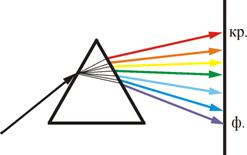
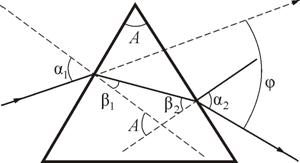
Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Рассмотрим дисперсию света в призме. Пусть монохроматический пучок света падает на призму с преломляющим углом А и показателем преломления n (рис.3.5.3) под углом .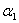

Рис.3.5.4.	Рис.3.5.3

После двукратного преломления (на левой и правой гранях призмы) луч оказывается преломлен от первоначального направления на угол φ. Очевидно, что угол отклонения лучей призмой зависит от показателя преломления n, а n – функция длины волны, поэтому лучи разных длин волн после прохождения призмы отклоняются на разные углы (рис.3.5.4). Пучок белого света за призмой разлагается в спектр, что и наблюдал Ньютон. Таким образом, с помощью призмы, разлагая свет на монохроматические составляющие, можно определить его спектральный состав.