Опыты Фарадея. Электромагнитная индукция

Только меняющееся со временем магнитное поле может породить электрический ток.

Опыты Фарадея состояли в следующем. Если постоянный магнит вдвигать внутрь катушки, к которой присоединен гальванометр, то в цепи возникает электрический ток. Если магнит выдвигать из катушки, гальванометр также показывает ток, но противоположного направления. Электрический ток возникает и в том случае, когда магнит неподвижен, а движется катушка (вверх или вниз). Как только движение прекращается, ток тотчас же исчезает. Однако не при всяком движении магнита (или катушки) возникает электрический ток. Если вращать магнит вокруг вертикальной оси, ток не возникает.

Гальванометр покажет наличие тока в катушке В при относительном перемещении ее и катушки А с током (рис. 3, а) в момент замыкания или размыкания ключа К или при изменении силы тока в цепи катушки А (при передвижении движка реостата, рис. 3, б). Нетрудно заметить, что ток в катушке возникает всякий раз, когда изменяется магнитный поток, пронизывающий катушку.

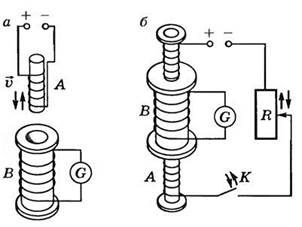
Рис. 3

Вывод: Такой ток называется индукционным (наведенным). В замкнутом контуре возникает индукционный ток только при изменении магнитного потока.

Явление возникновения ЭДС в проводящем контуре (тока, если контур замкнут) при изменении магнитного потока, пронизывающего контур, называется явлением электромагнитной индукции. Полученный таким способом ток называется индукционным током, а создающая его ЭДС — ЭДС индукции.

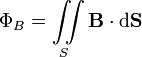Магни́тный пото́к — поток 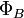как интеграл вектора магнитной индукции 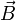через конечную поверхность 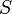. Определяется через интеграл по поверхности

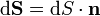при этом векторный элемент площади поверхности определяется как

где 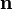— единичный вектор, нормальный к поверхности.

Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади:

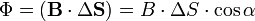
где α — угол между вектором магнитной индукции и нормалью к плоскости площади.

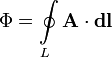Магнитный поток через контур также можно выразить через циркуляцию векторного потенциала магнитного поля по этому контуру: