Метод решения задач динамики

Уравнение (1.3.7) есть дифференциальное уравнение движения точки в векторном виде. Его решение — основная задача динамики материальной точки. При этом возможны две противоположные постановки задачи.

1. Найти действующую на точку силу 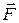, если известны масса m точки и зависимость от времени ее радиус-вектора 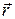(t).

2. Найти закон движения точки, т. е. зависимость от времени ее радиус-вектора 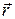(t), если известны масса m точки, действующая на нее сила 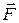(или силы 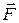_i) и начальные условия — скорость 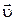₀ и положение 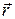₀ точки в начальный момент времени.

В первом случае задача сводится к дифференцированию 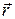(t) по времени, во втором — к интегрированию уравнения (1.3.7).

В зависимости от характера и постановки конкретной задачи решение уравнения (1.3.7) проводят или в векторной форме, или в координатах, или в проекциях на касательную и нормаль к траектории в данной точке. Выясним, как записывают уравнение (1.3.7) в последних двух случаях.