Третий закон Ньютона

Во всех случаях, когда в опыте участвуют только два тела A и B и тело A сообщает ускорение телу B, обнаруживается, что и тело B сообщает ускорение телу A. Отсюда мы заключаем, что действия тел друг на друга имеют характер взаимодействия.

Ньютон постулировал следующее общее свойство всех сил взаимодействия – третий закон Ньютона: силы, с которыми две материальные точки действуют друг на друга, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки:

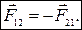(1.3.9)

Это значит, что силы взаимодействия всегда появляются парами. Обе силы приложены к разным материальным точкам и, кроме того, являются силами одной природы.

Закон (1.3.9) распространяется на системы из произвольного числа материальных точек. Мы исходим из представления, что и в этом случае взаимодействие сводится к силам попарного взаимодействия между материальными точками.

В третьем законе Ньютона предполагается, что обе силы равны по модулю в любой момент времени независимо от движения точек. Это утверждение соответствует ньютоновскому представлению о мгновенном распространении взаимодействий — предположению, которое носит название принципа дальнодействия ньютоновской механики. Согласно этому принципу, взаимодействие между телами распространяется в пространстве с бесконечно большой скоростью. Иначе говоря, если изменить положение (состояние) одного тела, то сразу же можно обнаружить хотя бы очень слабое изменение во взаимодействующих с ним телах, как бы далеко они ни находились.

В действительности это не так — существует конечная максимальная скорость распространения взаимодействий, которая равна скорости света в вакууме. Поэтому третий закон Ньютона (а также и второй) имеет определенные пределы применимости. Однако при скоростях тел, значительно меньших скорости света, с которыми имеет дело ньютоновская механика, оба закона выполняются с очень большой точностью. Свидетельством этому являются хотя бы расчеты траекторий планет и искусственных спутников, которые проводятся с «астрономической» точностью именно с помощью законов Ньютона.

Законы Ньютона являются основными законами механики. Они позволяют, по крайней мере, в принципе, решить любую механическую задачу; кроме того, из них могут быть выведены и все остальные законы механики.

В соответствии с принципом относительности Галилея законы механики одинаковы во всех инерциальных системах отсчета. Это значит, в частности, что уравнения (1.3.7) и (1.3.8) будут иметь один и тот же вид в любой инерциальной системе отсчета. Действительно, масса m материальной точки как таковой не зависит от скорости, т. е. одинакова во всех системах отсчета. Кроме того, для инерциальных систем отсчета одинаковым является и ускорение точки. Сила тоже не зависит от выбора системы отсчета, поскольку она определяется только взаимным расположением и скоростью материальной точки относительно окружающих тел, а эти величины, согласно нерелятивистской кинематике, в разных инерциальных системах отсчета одинаковы.

Таким образом, все три величины, входящие в уравнения (1.3.7) и (1.3.8), не меняются при переходе от одной инерциальной системы отсчета к другой, а,

следовательно, не меняются и сами уравнения. Другими словами, эти уравнения инвариантны относительно преобразований Галилея.

Виды взаимодействий и силы.

В современной физике различают четыре вида взаимодействия:

1. гравитационное или всемирное тяготение;

2. электромагнитное, осуществляемое через электромагнитные поля;

3. сильное или ядерное, обеспечивающее связь частиц в атомном ядре;

4. слабое, ответственное за процессы распада элементарных частиц.

В рамках классической механики имеют дело с первыми двумя видами. Два последних вида взаимодействий определяют взаимодействия элементарных частиц и играют существенную роль в микромире.

Приведем выражение для этих сил в самом простом виде, когда взаимодействующие массы или заряды покоятся или движутся с малой (нерелятивистской) скоростью.

Сила гравитационного притяжения действует между любыми двумя телами. Она обусловлена наличием у тел свойства, называемого гравитационной массы. Сила, действующая между материальными точками, в соответствии с законом всемирного тяготения, пропорциональна произведению масс точек m₁ и m₂, обратно пропорциональна квадрату расстояния r между ними и направлена по прямой, соединяющей эти точки:

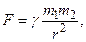(1.3.10)

где γ – гравитационная постоянная.

Фигурирующие в этом законе массы называют гравитационными в отличие от инертной массы, входящей во второй закон Ньютона. Из опыта, однако, установлено, что гравитационная и инертная массы любого тела строго пропорциональны друг другу. Поэтому можно считать их равными (т. е. выбрать один и тот же эталон для измерения обеих масс) и говорить просто о массе, которая выступает как мера инертности тела или как мера гравитационного действия. Взаимодействие происходит через гравитационное поле

Для тел конечных размеров и произвольной формы эта формула неприменима и гравитационная сила рассчитывается с помощью принципа суперпозиции. Однако для тел, масса которых распределена сферически симметрично, соотношение (1.3.10) справедливо. В этом случае r - расстояние между их центрами. Справедлива эта формула и в случае взаимодействия любого тела, находящегося на поверхности планеты (в частности Земли), с этой планетой. В этом случае тело можно считать материальной точкой. Тогда она примет вид

,

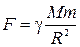где М – масса планеты (Земли), т – масса тела, R - радиус планеты. Направлена эта сила к центру планеты. Эта сила для данной планеты зависит только от массы тела. Тогда ее называют силой тяжести и записывают

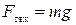, (1.3.11) где ускорение свободного падения 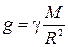. Направлена эта сила перпендикулярно поверхности планеты (вертикально). Если вводят силу тяжести, то полагают, что поверхность планеты – плоская (т.е. пренебрегают ее кривизной). Это справедливо, если перемещение по поверхности планеты невелико. Тогда гравитационное поле можно считать однородным и силу тяжести одинаковой во всех точках 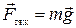. (1.3.12)

Несмотря на то, что гравитационные и электрические взаимодействия лежат в основе всего бесчисленного разнообразия механических явлений, анализ явлений, особенно макроскопических, оказался бы весьма сложным, если бы во всех случаях мы исходили из этих фундаментальных взаимодействий. Поэтому удобно ввести другие, приближенные, силы (которые в принципе могут быть получены из фундаментальных сил). Это необходимо для того, чтобы упростить математически задачу настолько, чтобы ее можно было практически решить.

С этой целью вводят, например, следующие силы, являющиеся результатом электромагнитного взаимодействия.

Упругая сила.

Под действием приложенных к нему сил всякое реальное тело деформируется, т.е. изменяет свои размеры и форму. Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называется упругой. Причиной возникновения этой силы является электромагнитное взаимодействие между частицами тела, которое изменяется при изменении расположения частиц, имеющих электрический заряд. Сила, действующая на одну частицу пропорциональна ее смещению из положения равновесия и направленная к положению равновесия: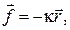

где 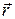— радиус-вектор, характеризующий смещение частицы из положения равновесия, 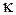- положительный коэффициент, зависящий от свойств и расположения частиц. Примером такой силы является сила упругой деформации при растяжении (сжатии) пружины или стержня. Если ввести координатную ось х вдоль пружины, то проекция силы упругости на эту ось

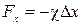, (1.3.13)

где 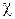- положительный коэффициент, называемый коэффициентом упругости или коэффициент жесткости, - деформация пружины, равная разности длин пружины в деформированном и недеформированном состоянии. Формула (1.3.13) называется законом Гука.

Этот же закон для однородного стержня при деформации растяжения (сжатия) можно записать иначе. Для этого вводят величины относительной деформации 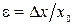и нормального напряжения 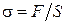( F - сила, действующая по нормали к сечению площадью S). Тогда закон Гука записывается 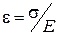(1.3.14)

Величина Е называется модулем Юнга. Она зависит от свойств материала.

Вес тела и сила нормальной реакции.

Вес 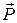— это сила, с которой тело действует на опору (или подвес), неподвижную относительно данного тела. Например, если тело с опорой (подвесом) неподвижны относительно Земли, то вес совпадает с силой тяжести.

Если тело взаимодействует с опорой (или подвесом), то они деформируются, в результате чего возникает сила. Однако, очень часто в таком случае величиной деформации пренебрегают, полагая тела недеформируемыми (абсолютно твердыми). Коэффициент жесткости, напротив, очень велик. В результате возникают силы, действующие на опору – вес тела и на тело – сила нормальной реакции опоры.

Сила трения скольжения. Эта сила возникает при скольжении одного тела по поверхности другого. Она также обусловлена деформацией неровностей поверхностей трущихся тел. Зависит эта сила от свойств поверхностей и того, насколько сильно они прижаты друг к другу:

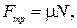(1.3.15)

где 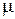— коэффициент трения скольжения, зависящий от природы и состояния соприкасающихся поверхностей (в частности, от их шероховатости); N — сила нормального давления, прижимающая трущиеся поверхности друг к другу. Сила F направлена в сторону, противоположную направлению движения данного тела относительно другого.

Сила сопротивления, действующая на тело при его поступательном движении в газе или жидкости. Эта сила зависит от скорости тела относительно среды, причем направлена противоположно вектору v:

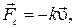(1.3.16)

где k — положительный коэффициент, характерный для данного тела и данной среды. Этот коэффициент зависит, вообще говоря, от скорости υ, однако при малых скоростях во многих случаях его можно практически считать постоянным.