Дифференциальные уравнения движения механической системы

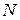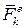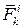Рассмотрим систему, состоящую из материальных точек (рис. 3. 4). Обозначим через и равнодействующие всех внешних и внутренних сил, приложенных к точке 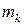. Составим для каждой точки системы дифференциальные уравнения движения:

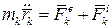, где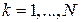

Рис. 3. 4. Движение произвольной точки механической системы

Полученные уравнения называются дифференциальными уравнениями движения системы материальных точек. Внутренние силы, входящие в эти уравнения, как правило, являются неизвестными. Интегрирование этих уравнений при известных внешних силах и начальном состоянии механической системы возможно в конечном виде лишь в исключительных случаях.

Основная роль уравнений движения системы состоит в том, что они являются исходными для вывода общих теорем динамики системы.