Сходящихся сил

Система сил, линии действия которых пересекаются в одной точ­ке, называется системой сходящихся сил.

Система сходящихся сил либо приводится к равнодействующей, либо находится в равновесии.

Теорема.Равнодействующая системы сходящихся сил равна век­торной сумме этих сил.

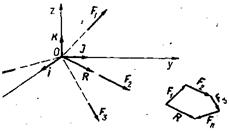
Действительно, пусть к абсолютно твердому телу приложена система сил F_1, F₂, ..., F_n, линии действия которых пересекаются в некоторой точке О (рис. 9). Мы могли бы складывать последова­тельно эти силы по аксиоме о параллелограмме сил. Однако этот путь очень длинен. Пользуясь правилом геометрического сложения векторов, сразу построим многоугольник сил F₁, F₂, ...,F_n, замыкающая сторона которого и будет равнодействующей силой R.

Изложенный способ определения равнодействующей является геометрическим. Однако равнодействующую силу R можно определить и аналитически, по проекциям на неподвижные оси декартовой системы координат, выбрав за начало координат точку О пересечения линий действия системы сходящихся сил.

Равновесие системы сходящихся сил.

Условия равновесия системы сходящихся сил

Если система сходящихся сил находится в равновесии, механи­ческим условием равновесия является равенство нулю равнодейст­вующей силы. Получим

или R = 0

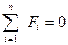
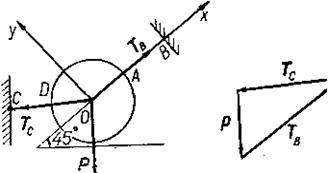
Так как векторная сумма сил равна нулю, то многоугольник сил является замкнутым (начало первого вектора силы и конец по­следнего совпадают).

Таким образом, при равновесии системы сходящихся сил много­угольник сил является замкнутым (условие равновесия в геометри­ческой или графической форме).

В аналитической форме условия равновесия системы сходящихся сил заключаются в следующем.

Если пространственная система сходящихся сил находится в рав­новесии, то алгебраическая сумма проекций этих сил на каждую из трех координатных осей должна равняться нулю (на две оси, если система сходящихся сил расположена на плоскости).

Поскольку в случае равновесия указанной системы сил их рав­нодействующая равна нулю (R = 0), то равны нулю и ее проекции на оси координат, т. е. R_х = 0, R_у = 0, R_г = 0. На основании (1.10) получим

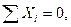
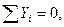
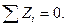
Для плоской сходящейся системы сил имеем

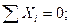
Условия (1.13) и (1.14) в аналитической форме называются также уравнениями равновесия. Для статической определенности задачи число неизвестных не должно превышать числа уравнений равно­весия.

Моментом силы относительно точки называется векторное произведение радиус-вектора точки приложения силы на силу. Итак, по определению (рис. 12),

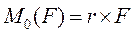
Обозначая длину перпендикуляра, опущенного из центра момента на линию действия силы, через h (величину h в дальнейшем будем называть плечом), можно модуль вектора Мо (F) представить в виде произведения Fh, т. е.

|М₀(F)| =М₀(F) = Fh.

Таким образом, момент силы относительно точки — это вектор, направленный перпендикулярно к плоскости, содержащей силу и точку, в ту часть пространства,.

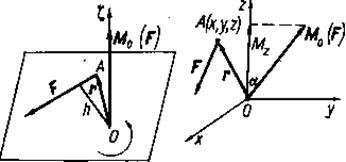
Для аналитического определения момента силы относительно точки выберем произвольную систему координат О_xyz с началом в точке О (рис. 13) и обозначим проекции радиуса-вектора г и силы F на координатные оси О_x, О_Y, О_z, соответственно через х, у, z и X, У, Z. Заметим, что проекции х, у, z радиуса-вектора г точки прило­жения силы одновременно означают координаты этой точки. Тогда, спроектировав обе части векторного равенства (1.15) на оси координат, получим выражение момента силы относительно точки в анали­тической форме в виде трех его проекций на координатные оси:

,

.

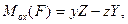
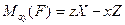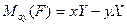Теорема о моменте равнодействующей системы

сходящихся сил (теорема Вариньона)

Момент силы относительно оси

Моментом силы относительно оси называется проекция на ату ось момента силы относительно произвольной точки на оси. Момент силы F относительно оси Оz обозначается через М_z (F). Таким обра­зом,

М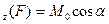

Момент силы относительно оси, как будет показано в динамике, является физической величиной, характеризующей вращательное движение твердого тела.

Согласно определению, моменты силы относительно координат­ных осей выражаются величинами (1.18), т. е. соответственно равны проекциям

М 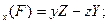М_У(F) = zХ -хZ; М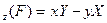

Укажем практический способ определения момента силы относи­тельно оси.