Уравнения (1.36) выражают механические условия равновесия произвольной пространственной системы сил (свободного твердого тела).
Условия равновесия произвольной пространственной системы сил можно выразить в геометрической форме: многоугольники сил и моментов этих сил должны быть замкнутыми.
При равновесии векторы R и Мо равны нулю, следовательно, равны нулю и их проекции на координатные оси. На основании формул (1.25) и (1.27) получим условия равновесия произвольной пространственной системы сил в аналитической форме:

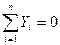
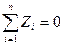
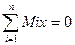
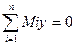
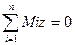
Произвольная пространственная система сил (свободное твердое тело) находится в равновесии, когда алгебраические суммы проекций всех сил на три координатные оси и алгебраические суммы моментов этих сил относительно координатных осей равны нулю
Условия равновесия, выраженные в аналитической форме, называются также уравнениями равновесия. Если число неизвестных превышает число уравнений равновесия, то задача является статически неопределенной.
2. Условия равновесия сил, произвольно расположенных в одной
плоскости.
Рассмотрим произвольную систему сил, расположенных в одной плоскости (рис. 18). Для удобства исследования совместим с этой плоскостью координатную плоскость Оху. Тогда из шести уравнений (1.37) третье, четвертое и пятое обратятся в тождества.
Таким образом, произвольная система сил, расположенных в одной плоскости, уравновешивается лишь в том случае, когда алгебраические суммы проекций всех сил на две координатные оси (Ох и Оу) и алгебраическая сумма моментов сил относительно произвольной точки этой плоскости равны нулю:
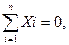
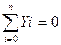
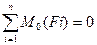
Условия (1.38) называются уравнениями равновесия произвольной системы сил на плоскости. Для статической определенности задачи необходимо, чтобы число неизвестных не превышало трех.
Заметим, что форму уравнений равновесия можно изменить, но нельзя изменить их количества, так как оно соответствует механическим условиям равновесия. Можно составить одно уравнение проекций сил на одну из координатных осей (например, Ох) и два уравнения моментов сил относительно двух точек А u В, лежащих в плоскости действия сил, причем прямая АВ не должна быть перпендикулярной к оси Ох, а именно!
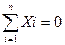 ,
, 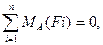
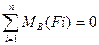
Дата добавления: 2015-08-08; просмотров: 987;
