Приведение пространственной системы сил к равнодействующей

Если главный вектор R и главный момент Мо системы сил вза­имно перпендикулярны, то пространственная система сил приво­дится к равнодействующей. Действительно, пусть в точке О угол φ между R и Мо (рис. 21) равен 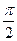. Главный момент Мо заменяем парой из сил (R, —R) и с плечом 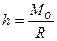.В точке О силы (R и —R) уравновешиваются и остается равнодейст­вующая сила R, приложенная в точке А.

Докажем теорему Вариньона о моменте равнодействую­щей в общем виде.

Если пространственная система сил имеет равно­действующую, то ее момент относительно некоторой точ­ки равен векторной сумме моментов составляющих сил. Действительно, момент равнодействующей R относительно точки О (рис. 21) равен Мо (R) = hR, но h = 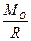, где Мо — величина