Приведение пространственной системы сил к паре
Если главный вектор R = 0, а главный момент системы сил Мо не равен нулю, то система сил приводится к паре. Момент этой пары равен главному моменту рассматриваемой системы сил:
М = М0 = 
В частности, произвольная система пар сил эквивалентна одной паре сил, момент которой равен геометрической сумме моментов всех пар сил системы (теорема о сложении пар сил):
M= 
Отсюда следует, что произвольная система пар сил уравновешивается, когда векторная сумма моментов пар сил составляющих равна нулю, т. е. когда многоугольник моментов пар сил является замкнутым (условие равновесия системы пар сил):
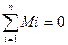
Если все пары сил системы расположены в одной плоскости, то в случае ее равновесия алгебраическая сумма моментов пар сил составляющих равна нулю.
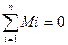
Центр параллельных сил. Центр тяжести
Центр параллельных сил
Центром параллельных сил называется точка на линии действия ее равнодействующей, не изменяющая своего положения при повороте всех сил на один и тот же угол вокруг их точек приложения.
Пусть задана система параллельных сил F1, F2, ..., Fn, соответственно приложенных в точках А1(х1, у1, z1), А2 (х2, у2, z2),:.. ..., Аn (хn, уn, zn) (рис. 29). Проекция равнодействующей этой системы сил на ось 2, параллельную им, равна алгебраической сумме проекций составляющих сил:
Rz=  , или R=
, или R= 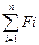
Зная координаты точек приложения параллельных сил, определим положение центра параллельных сил, применив теорему Вариньона о моменте равнодействующей.
Для определения координаты хс центра параллельных сил составим уравнение моментов сил относительно оси у. Получим
Му(R)= 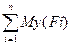
Или
Rxc= 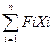
Откуда
Xc= 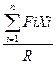
Дата добавления: 2015-08-08; просмотров: 1840;
