Распространенные на весь объем V тела М. Таким образом,

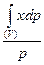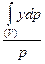Xc= , Yc= , Zc= ,

Центр тяжести однородного тела

Если тело однородно, то удельный вес его постоянный (γ=const). Тогда вес тела р будет равен р = γV , а dр = γdV. Здесь V обозначает объем тела, dV — элементарный объем. Подставляя эти значения в формулы (1.53), получим выражения для координат центра тяжести однородного тела:

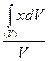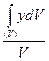Xc= , Yc= , Zc= ,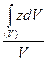

Как видно из формул (1.54), центр тяжести однородного тела является центром тяжести его объема. Интегралы, стоящие в числи­телях формул (1.54), называются статическими моментами объема тела относительно соответствующих координатных плоскостей. Так, интеграл 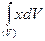есть статический момент тела относительно плоскости Оуz, интеграл 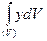— относительно Охz и интеграл 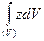—относительно плоскости Оху.

Центр тяжести площади плоской фигуры

Определение центра тяжести площади плоской фигуры в теоретической механике представляет особый интерес. Здесь возможны два случая: 1) плоская фигура ограничена ломаной линией (рис 31); 2) плоская фигура ограничена криволинейным контуром (рис 32). В первом случае фигуру разбивают на элементарные фигуры, положение центров тяжести которых известны, и применяют формулы для координат центра параллельных сил (1.51).

В случае однородной плоской фигуры сила тяжести пропорциональна ее площади р=γS, где S – площадь, γ – вес единицы площади. Тогда получим:

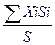Xc= , Yc=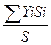

Если плоская фигура ограничена криволинейным контуром, то получим:

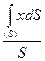Xc= , Yc=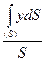

где интеграл 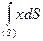, распространенный на всю площадь плоской фигуры, называется статическим моментом этой площади относительно оси у и

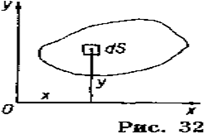
обозначается через Му. Соответственно интеграл 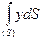называется статическим моментом площади Sплоской фигуры относительно оси х и обозначается через Мх, т.е.

Мх= 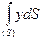, Му= .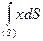

Таким образом, формулы (1,56) принимает вид

Хс= 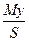, Yc= .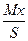

Центр тяжести линии

К этому понятию приходим, рассматривая однородное тело, например проволоку, с постоянной площадью поперечного сечения а и длинной l.

Итак, пусть требуется определить координаты центра тяжести линии АВ длиною l (рис 33). В случае однородной линии ее вес пропорционален длине (р=γ l), вес элемента dр = γdl, γ — вес единицы длины (γ = сonst). Следова­тельно, по формулам (1.53) получим

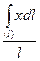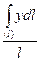Xc= , Yc= , Zc=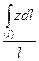

Интегралы в (1.58) являются криволинейными

Графическое нахождение центра тяжести площади плоской фигуры

Положение центра тяжести площади плоской фигуры можно определить графически, как точку пересечения линий действия рав­нодействующих параллельных сил тяжести элементарных фигур, на которые расчленена рассматриваемая плоская фигура в данном положении и в повернутом на некоторый угол. Определяя графически центр тяжести площади плоской фигуры, сле­дует придерживаться такой последовательности:

1) разбить рассматриваемую фигуру на элементарные, положение центров тяжести, которых можно легко опреде­лить;

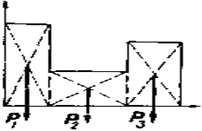
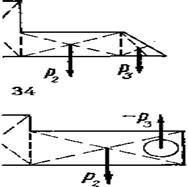
2) измерив площади всех указанных фигур в выбран­ном масштабе, приложить их силы тяжести, которые пропор­циональны соответствующим площадям (рис. 34), т. е. р₁ = kS₁; р₂ = kS₂; ...; р_n = kS_n, где (k — коэффициент пропорциональности. Если при этом рассматриваемая плос­кая фигура содержит вырезанные площади (отверстия), то соответствующие силы тяжести, как вычитаемые силы, сле­дует направить вертикально вверх (рис. 35);

3) далее нужно обозначить параллельные силы соответственно полями и с помощью веревочного многоугольника опре­делить линию действия равнодействующей;

4) повернув все силы на один и тот же угол, вновь следует опре­делить линию действия равнодействующей. Точка пересечения С указанных линий действия равнодействующих является центром тяжести рассматриваемой фигуры