Формирование понятия геометрической фигуры
Исторически понятие геометрической фигуры, так же как понятие натурального числа, было одним из исходных понятий математики. Как и натуральные числа, понятие геометрической фигуры образовалось с помощью абстракции отождествления, в основе которой лежит некоторое отношение эквивалентности. В данном случае таким отношением является «сходство», «подобие» предметов по их форме, с помощью которого множество предметов разбивается на классы эквивалентности так, что любые два предмета одного класса имеют одинаковую форму, а любые два предмета различных классов — различные формы. Абстрагируясь при этом от других свойств предметов (цвета, величины, материала, из которого они сделаны, назначения и т. д.), мы получаем самостоятельное понятие геометрической фигуры.
В математике поступают и так: класс подобных по форме предметов определяется любым принадлежащим ему предметом и называется формой.
В связи с рассмотрением отношения эквивалентности (глава IV, § 4) был приведен пример классификации блоков по их форме. Решая эту задачу, дети получают классы квадратных, круглых, треугольных и прямоугольных блоков, затем каждый из этих классов, так же как и отдельные их представители, называются соответственно квадратом, кругом, треугольником, прямоугольником. В основе выделения этих понятий лежит отношение эквивалентности
«иметь одинаковую форму».
В изучении геометрии, и в частности геометрических фигур,
различают несколько уровней мышления.
Первый, самый простейший уровень характеризуется тем, что геометрические фигуры рассматриваются как целые и различаются только по своей форме. Если показать дошкольнику круг, квадрат, прямоугольник и сообщить ему соответствующие названия, 1 то после некоторого времени он сможет безошибочно распознавать } эти фигуры исключительно по их форме (причем еще не аиалиаиро-ванной), не отличая квадрат от прямоугольника. На этом уровне квадрат противопоставляется прямоугольнику.
На следующем, втором, уровне проводится анализ воспринимаемых форм, в результате которого выявляются их свойства. Геометрические фигуры выступают уже как носители своих свойств и распознаются по этим свойствам, свойства фигур логически еще не упорядочены, они устанавливаются эмпирическим путем. Сами фигуры также не упорядочены, так как они только описываются, но не определяются. Этот уровень мышления в области геометрии еще не включает структуру логического следования.
©писанные выше два уровня вполне доступны детям 4—6 лет, и это обстоятельство следует учитывать при составлении программ «Лучения и разработке методики.
Из чего состоит геометрическая фигура?
Всякая геометрическая фигура подразумевается состоящей из точек, т. е. всякая геометрическая фигура представляет собой множество точек, ъ том числе одну точку тоже принято считать
геометрической фигурой.
Поэтому операции над множествами и отношения между множествами, рассмотренные в главе Ш, можно переносить на геометрические фигуры как на множества точек.
Например, на рисунке 11 изображены •всевозможные отношения, в которых могут находиться квадрат и круг:
/ — круг находится в квадрате;
— квадрат находится в круге;
— квадрат и круг пересекаются;
— квадрат и круг не пересекаются.
Предлагая детям располагать квадрат и круг всевозможными способами или нарисовать их и закрашивать общую часть (пересечение) определенным цветом, тем самым помогаем им выявить особенности каждого из отношений, изображенных на рисунке И:
а) все точки круга являются точками -квадрата;
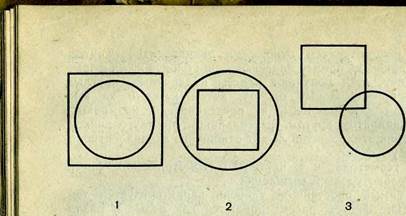
|
|

Рис. 11.
б) все точки квадрата являются также точками круга;
в) квадрат и круг имеют общие и необщие точки;
г) у квадрата и круга нет общих точек.
На предматематическом уровне дети знакомятся с простейшими, но наиболее . распространенными геометрическими фигурами: различными линиями, формами блоков — квадратом, кругом, треугольником, а также пятиугольником, шестиугольником. Строгих определений, разумеется, на этом уровне не дается.
 § 2. Виды геометрических фигур
§ 2. Виды геометрических фигур
Будем рассматривать далее лишь те виды простейших геометрических фигур, с которыми приходится иметь дело в процессе обучения дошкольников.
Все геометрические фигуры делятся на плоские и пространственные. Так, например, квадрат, круг — плоские фигуры; куб, шар — пространственные. Начнем с рассмотрения линий. Под линией будем иметь в виду плоскую линию -т- линию, все точки которой лежат на некоторой плоскости, а сама линия есть подмножество точек плоскости.
Очевидно, что такие разъяснения, как «длина без ширины» или «граница поверхности», не могут приниматься за точные определения, так как мы не знаем точный смысл терминов «длина», «ширина», «граница», «поверхность» и т. п. По существу в элементарной геометрии понятие линии считается интуитивно ясным и их изучение, сводится к рассмотрению различных примеров: прямая, ломаная, кривая, замкнутая линия, незамкнутая линия, отрезок и др.
Прямую линию, или просто прямую, можно выделить среди других линий с помощью ее характеристических свойств, т. е. таких свойств, которыми обладает только прямая и никакие другие линии.
На рисунке 12 между деревом и домом проложено несколько тропинок. На геометрическом языке это означает: через две точки D и С проходит несколько линий. Прямая выделяется среди них тем, что это — линия кратчайшего расстояния.
| Рис. 13. |
Еще одно характеристическое свойство прямой: через две точки D и С можно провести много различных линий, прямых — только одну, т. е. через две точки проходит одна и только одна
прямая.
Линии бывают замкнутыми и незамкнутыми. Например, прямая — незамкнутая линия, окружность — замкнутая.
По отношению к прямой две точки могут находиться «по одну сторону» от нее или «по разные стороны». Например, дом и дерево могут находиться по одну сторону от речки и тогда можно дойти от дома до дерева или обратно, не проходя через мост. Если же они находятся по разным сторонам от реки, то дойти от дома до сада или обратно, не проходя через мост, нельзя.
На геометрическом языке эта ситуация описывается следую-
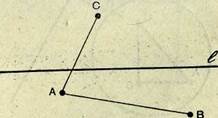
Sf; щим образом. Две точки А к В находятся по одну сторону от
прямой /, если отрезок, соединяющий эти точки, не пересекает
прямую / (рис. 13).
Две точки Л и С (рис. 13) находятся по разные стороны от прямой /, если отрезок Л С, соединяющий эти точки, пересекает
прямую I.
По существу прямая I разбивает множество всех не принадлежащих ей точек плоскости на два класса (два подмножества), называемые п о л уплоскост я м и с границей /. Это разбиение порождается отношением эквивалентности, введенным в множество всех не принадлежащих / точек плоскости следующим образом: две точки находятся в этом отношении, если отрезок, соединяющий их, не пересекает прямую /, и не находятся в этом отношении, если этот отрезок пересекает прямую /.
Дети довольно рано усваивают, что означает «внутри» и «вне» некоторой замкнутой линии. Пример этого — детская игра в классы. Чтобы успешно переходить из класса в класс, нужно, прыгая и бросая биту, точно попадать внутрь определенного класса (квадрата). Первые представления о «внутри» и «вне» закрепляются в играх с обручами (глава III), когда дети встречаются со все усложняющимися ситуациями 
определение блоков внутри и вне одного обруча, внутри одного и вне другого обруча, внутри всех трех обручей, внутри двух обручей и вне третьего и т. п. Поэтому перед решением задач, связанных с- классификацией блоков, или фигур в играх с обручами необходимо выяснить, распознают ли дети внутреннюю и внешнюю области по отношению к каждому обручу.
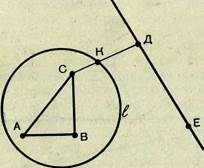
Переведем теперь эти ситуации на язык геометрии. Интуитивно ясно, что всякая окружность разбивает множество всех не принадлежащих ей точек плоскости на две области (рис. 14). Если две точки Л и В или D и Е лежат в одной области, то отрезок, соединяющий их, не пересекает линии /; если две точки, например С и D, принадлежат различным областям, то соединяющий их отрезок пересекает линию / (в точке К)-
Одна из этих областей называется внутренней, другая — внешней. Каким же геометрическим свойством можно охарактеризовать внутреннюю или внешнюю область?
Область, которая интуитивно принимается за внешнюю, обладает следующим свойством: можно найти в этой области две точки, например D и Е, такие, что прямая, проходящая через них, целиком лежит в этой области. Вторая область, которая интуитивно принимается за внутреннюю, не обладает этим свойством или характеризуется свойством, представляющим собой отрицание характеристического свойства внешней области, т. е. нельзя найти в ней такие две точки, чтобы прямая, проходящая через них, лежала целиком в этой области (или, иначе, прямая, проходящая через любые две точки этой области, обязательно пересекает линию /).
Выше мы пользовались понятием «отрезок» и связывали его неизменно с двумя точками: «отрезок АВ», «отрезок, соединяющий точки Л и В» и т. п. Что же такое отрезок? Иногда говорят «часть прямой». Это можно понимать как подмножество точек прямой. Но какое это подмножество?
Иногда пользуются отношением «между», применимым к трем
|
| Рис. 14. |
точкам. Это отношение соответствует наглядному представлению о точке, лежащей на прямой между двумя другими точками: если точка С лежит между точками А и В, то нельзя «дойти» по прямой от Л к В, не пройдя через точку С. Эти наглядные представления подсказывают и некоторые свойства отношения «между»: если точка С лежит между А и В, то С лежит и между В и Л; из трех точек только одна лежит между двумя другими, т. е. если С лежит между Л и В, то уже А
не лежит между С и В, а также В не лежит между А и С.
Имеются две различные трактовки понятия отрезка {ш существу два различных понятия). По одной из них отрезку АВ принадлежат сами точки Л и В (концы отрезка) и все точки прямой АВ, лежащие между А и В. По другой трактовке точки А я В не считаются принадлежащими отрезку АВ, хотя по-прежнему называются его концами (т. е. концы отрезка не принадлежат
ему).
Мы будем придерживаться первой трактовки, дидактически
более целесообразной.
Так как через две точки Л и В проходит единственная прямая АВ, то эти две точки определяют и единственный отрезок с
концами Л и В.
Зная, что такое отрезок, можно уточнить и понятие ломаной
линии.
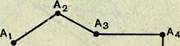
Если Ль Л2, Аъ,... , А„_!, Ап — точки, никакие последовательные три из которых не лежат на одной прямой, то линия, состоящая из отрезков Л1Л2, Л2Л3, ..., ЛП-|Л„, называется ломаной линией, эти отрезки называются звеньями ломаной, а точки Ль Аъ, Аг, ..., Ап-\, Л„ — ее вершинами, точки А\ и Ап называются также концами ломаной.
Если концы ломаной совпадают, то ломаная называется з а м к-н у т о й, в противном случае — «е замкну той (строгие определения замкнутой и незамкнутой кривой линии в элементарной
геометрии не даются).
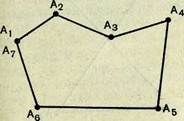
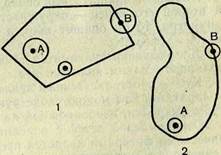
На рисунке 15, 1 изображена замкнутая ломаная линия, на
рисунке 15,2 — незамкнутая.
Как и всякая замкнутая линия, замкнутая ломаная линия разбивает множество не принадлежащих ей точек плоскости на две области — внутреннюю и внешнюю.
Среди ломаных линий выделяют простые (без самопересечений) ломаные линии, т. е. такие, которые сами себя не пересекают.
|
|
Изображенные на рисунке 15 ломаные линии простые. На
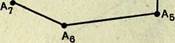
Р«с. 15
рисунке 16,/, 2 изображены непростые, сами себя пересекающие ломаные линии.
Перейдем теперь к рассмотрению многоугольников. Имеются два основных подхода, по существу определяющих различные понятия: согласно одному из них под многоугольником понимают простую замкнутую ломаную линию, согласно второму — простую замкнутую ломаную вместе с ее внутренней областью или объединение простой замкнутой ломаной и ее внутренней области.
Согласно первой трактовке модель многоугольника, например, можно изготовить из проволоки, по второй — вырезать из бумаги. Какая же из двух трактовок более целесообразна с дидактической точки зрения? (С логической точки зрения обе трактовки корректны и имеют право на существование.) Для маленьких детей более естественным является называть квадратом, треугольником и т. д. именно ту фигуру, которую они закрасили и вырезали, т. е. ломаную вместе с ее внутренней областью. Поэтому представляется, что и для школы вторая трактовка является более целесообразной.
Многоугольники классифицируются по числу сторон или углов: треугольники, четырехугольники, пятиугольники, шестиугольники и т. д. Наблюдая различные многоугольники, можно обнаружить наличие или отсутствие свойства, называемого выпуклостью.
На рисунке 17 изображены многоугольники, обладающие (в случаях /, 2, 4, 6) и не обладающие (в случаях 3, 5, 7) этим свойством.
| Рис. 16. |
Как же геометрически описать это интуитивно ясное свойство? Любой из многоугольников в случаях /, 2, 4, 6 (рис. 17) расположен по одну сторону от прямой, проведенной через каждую его сторону, т. е. если продолжить любую сторону, полученная прямая не пересечет многоугольник (с этой целью на рисунке стороны этих многоугольников продолжены пунктиром). В каждом из многоугольников в случаях 3, 5, 7 существует хотя бы одна такая сторона, продолжение которой пересекает многоугольник. Первые называются выпуклыми, вторые — невыпуклыми.'
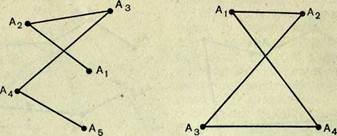
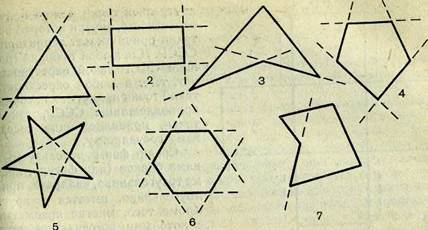
Рис. 17.
Треугольник, квадрат, прямоугольник — выпуклые четырехугольники. Пятиконечная звездочка — невыпуклый десятиугольник.
Стороны, включая вершины, многоугольника, т. е. замкнутая ломаная, образуют границу многоугольника. Это интуитивно ясное понятие. Например, интуитивное представление о границе фигуры готовит детей к географическому понятию границы.
Чем же отличается граничная точка, т. е. точка, принадлежащая границе, от внутренней точки многоугольника (и вообще фигуры)? Как это различие описать геометрически?
С этой целью введем понятие окрестности точки. Под окрестностью точки А будем понимать круг любого радиуса с центром в точке А. Теперь, пользуясь этим весьма наглядным понятием, опишем различие между внутренней и граничной точками многоугольника.
Для любой внутренней точки А, как бы близка она ни была к границе, всегда можно найти окрестность, все точки которой внутренние (рис. 18, 1,2).
Для граничной точки В нет такой окрестности, т. е. какую бы окрестность точки В ни взяли, внутри ее найдутся как внутренние, так и внешние точки. Такими же свойствами обладают внутренние и граничные точки на географической карте, представляющей собой некоторую геометрическую фигуру.
|
Например, на географической карте СССР для любой рис. 18.

| VII. ВЕЛИЧИНЫ И ИХ ИЗМЕРЕНИЕ |
| Глава |
внутренней точки можно найти окрестность, внутри которой все точки принадлежат территории СССР. Для любой точки на границе СССР такой окрестности нет, т. е. в любой окрестности такой точки найдутся как точки, принадлежащие СССР, так и точки, принадлежащие соседнему государству.
Среди форм используемых нами блоков (или фигур), кроме треугольника, квадрата, прямоугольника, имеется и круг. Кроме того, многие предметы, с которыми встречаются дети (тарелки, блюдца, колеса велосипеда и др.), имеют круглую форму. Считаем нецелесообразным для дошкольников вводить термин «окружность».
В элементарной геометрии круг определяется как множество (или геометрическое место) всех точек плоскости, удаленных от некоторой точки, называемой центром, на расстояние, не превышающее R (/? —радиус круга); окружность определяется аналогично как множество всех точек плоскости, удаленных от точки, называемой центром, на одно и то же расстояние R.
| Рис. 19. |
Заметим, что если в этих формулировках слово «плоскость» заменить словом «пространство», то получим определения шара и сферы, соответственно пространственных аналогов круга и окружности. Круг, окружность, шар и сферу можно определить и генетически, т. е. описанием процесса образования этих фигур. Этот процесс легко смоделировать: если отрезок зафиксировать в одном конце и вращать его около этого конца, то он опишет круг, а второй его конец — окружность. Если полукруг вращать около диаметра, то он опишет шар, а ограничивающая его полуокружность — сферу.
Дошкольники знакомятся также с одним из простейших многогранников, каким является куб.
Куб — пространственный аналог квадрата. Он ограничен шестью квадратами. Его можно сконструировать (склеить) из плоской фигуры выкройки, изображенной на рисунке 19.
Ознакомление детей с описанными выше простейшими геометрическими фигурами является пропедевтической основой для дальнейшего формирования и развития у них геометрических, в том числе пространственных, представлений.
Дата добавления: 2015-07-10; просмотров: 4232;
