Основные идеи количественной теории натуральных чисел
В количественной теории натуральное число с самого начала воспринимается как число элементов (мощность, численность) конечного множества.
Что такое конечное множество? Для разъяснения одного из возможных определений воспользуемся интуитивными представлениями бесконечного и конечного множества, в частности о натуральном ряде 1, 2, 3, ...в качестве образца бесконечного множества и его правильной части (подмножества) четных чисел 2, 4, 6, ... .
Вопрос «Каких чисел больше: всех натуральных или всех четных?» кажется тривиальным, а правильный ответ парадоксальным.
Действительно, можно установить взаимно однозначное соответствие между элементами этих двух множеств:
1, 2, 3... к,...
2, 4, 6, ..., 2л,...
откуда интуитивно ясно, что четных чисел ровно столько, сколько и всех натуральных чисел.
Парадоксальность этого результата связана с тем, что такое соответствие возможно лишь в случае бесконечного множества.
Если же взять какое-нибудь конечное множество, то не удастся установить взаимно однозначное соответствие между всем множеством и какой-нибудь его (правильной, т. е. не совпадающей со всем множеством) частью.
Это, как правило, является определяющей характеристикой конечного множества.
Таким образом можно определить конечное множество: множество А называется конечным, если нельзя установить взаимно однозначное соответствие между всем этим множеством и какой-нибудь его правильной частью.
Рассмотрим теперь всевозможные конечные множества (говорят «класс или семейство множеств») и установим для них отношение эквивалентности следующим образом: два множества А и В будем называть эквивалентными (обозначается это через А~В), если между элементами этих множеств можно установить взаимно однозначное соответствие.
Установленное таким образом отношение множеств является отношением типа эквивалентности, т. е. рефлексивно, симметрично и транзитивно: для любых множеств Л, В, С:
а) А~А; б) если А~В, то В~Л; в) если А~В и В~С, то А~С.
Поэтому введенное отношение порождает разбиение данного семейства множеств на классы эквивалентности так, что любые два множества одного класса эквивалентны, а любые два множества различных классов неэквивалентны.
Эквивалентные множества не совпадают полностью, всеми своими свойствами: множество пальцев человеческой руки и множество, состоящее из пяти столов, различные, но эквивалентные множества.
Каждый класс эквивалентности характеризуется мощностью, т. е. любые два множества одного класса равномощны (имеют одинаковую мощность). Так как мы имеем дело лишь с конечными множествами, то равномощность означает равночисленность. Мощность или класс равночисленных конечных множеств и называют натуральным числом.
Таким образом, каждому конечному множеству А приписывают в качестве характеристики натуральное число m (Л), определяющее его принадлежность определенному классу эквивалентности. При этом множествам, принадлежащим одному классу эквивалентности, приписывается одно и то же натуральное число:
если Л ~ В, то m{A) — m(B),
множествам, принадлежащим различным классам эквивалентности,— различные натуральные числа:
если А^В, то т(А)Фт{В).
Так как А и В — конечные множества, то натуральные числа m (Л) и т (В) обозначают числа элементов (численность) этих множеств.
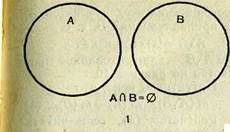
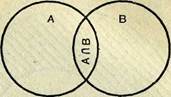 Рис. 9.
Рис. 9.
В основе такой концепции натурального числа лежит абстракция отождествления: отношение эквивалентности множеств отождествляет множества, принадлежащие одному классу эквивалентности по их численности.
В результате этого отождествления от множеств, принадлежащих одному классу эквивалентности, абстрагируется их общее свойство, характеризующее этот класс, в виде самостоятельного понятия — натурального числа.
Название «количественная теория» связано с тем, что в этой теории натуральное число обозначает количество элементов множества.
Достоинством этого подхода является естественное, отражающее основной круг практических применений сложение, вычитание и умножение натуральных чисел.
I. Если ЛПВ=0, то т(ЛиВ) = т(Л) + т(В), (1)
т. е. если Л и В — конечные непересекающиеся множества, то число элементов объединения этих множеств равно сумме чисел их элементов (см. рис. 9, /). Сложение чисел абстрагируется от объединения множеств, что и используется в обучении детей дошкольного возраста.
Если же множества Л и В пересекающиеся, т. е. А{]ВФ0 (рис. 9, 2), то нетрудно заметить, что
так как в сумме т (А) + т (В) число элементов пересечения т. (Л (]В) учитывается дважды: один раз в числе т (Л), второй раз в числе т{В).
Равенство (1), если читать его справа налево, может служить определением суммы двух натуральных чисел:
суммой натуральных чисел а и b называется число а + Ь —
= т(Л11В), где Л и В — произвольные конечные множества такие,
что т(Л) = а, т(В) = Ь и ЛПВ=0. (3)
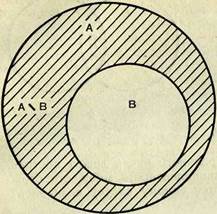
II. Пусть теперь Л и В — два произвольных конечных множества, причем В^А (рис. 10).
Разность множеств Л и В, обозначаемая А\В, есть множество,
|
состоящее из всех элементов А, не принадлежащих В, т. е. А\В = {х\х£А и х£В), где А\В — заштрихованное множество на рисунке 10.
Интуитивно ясно, что т {А\В) = т(А)-т(В). (4)
| Рис. 10. |
Равенство (4), если . читать его справа налево, служит основой для определения разности двух натуральных чисел: разность двух натуральных чисел а и Ь, где а ^ Ь определяется равенством а — Ь — т(А\В), где А а В — произвольные конечные множества, удовлетворяющие условиям
т{А) = а, т{В)=Ъ и В^А. (5)
III. Выше (глава IV, § 2) мы видели на примерах, что число
элементов декартового произведения АХВ двух конечных множеств
А а В можно сосчитать как число клеток соответствующей
III таблицы пар. Так, в примере I число элементов множества А
(городов) — 8, а число элементов множества В (рек) — 4, а следо-
111 вательно, множество всевозможных пар (город, река), т. е. эле-
ментов АХВ или клеток таблицы,— 32.
Известно, например, что поля шахматной доски обозначаются парами элементов двух множеств А = {а, Ъ, с, d, e, f, g, h} и В = {\, 2, 3, 4, 5, 6, 7, 8}, т. е. каждое поле можно рассматривать как элемент декартового произведения Л X В и, так как т (Л) = 8, и т(В) = 8, то т(ЛхВ)=64, т. е. т(А) т(В).
Обобщая эти конкретные случаи, получаем:
т(АхВ) = т(А) т(В). (6)
Равенство (6) может служить определением произведения двух
натуральных чисел:
а-Ь = т{АХВ),
где Л и В — произвольные множества, удовлетворяющие условиям т(А) = а и т(В) = Ь.
Из данного определения можно получить другое, сводящее умножение к сложению одинаковых слагаемых. Достаточно считать клетки таблицы или пары, расположенные в прямоугольной таблице, рядами. В каждом ряду m (Л) клеток, а рядов столько, сколько элементов в множестве В, т. е. т (В). Значит, всего клеток т(А)-\~... + т(А), или а-\-а-\-... +
т(В)
Л эта сумма равна т(АХВ). Но согласно приведенному выше определению m{AxB) = ab. Следовательно,
b
Если применить этот способ образования или подсчета пар к приведенному выше примеру именования полей шахматной доски,
то получим:
а\, Ы, сХ, d\, el, f\, gl, hi, m{A) m(B) J ей, Ь2, c2, d2, e2, /2, g2, hi, m{A)
| a8, |
| e. |
cB, dB, e8, fB, gB, hB,.m(A)
m (B)
Далее мы обратимся еще раз к описанной выше концепции натурального числа, когда будет возможность сравнить ее с другой, разработанной в математике порядковой теорией натуральных чисел с целью выяснения наиболее приемлемой и целесообразной методики обучения.
Дата добавления: 2015-07-10; просмотров: 2892;
