Свойства отношений

1. Рассмотрим еще один пример отношения.

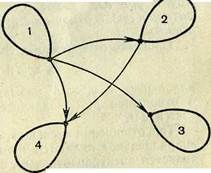
Если А = {\, 2, 3, 4}и Р = {(1, 1), (1, 2), (1,3), (1, 4), (2, 2), (2, 4), (3, 3), (4, 4),Чо р — (Р, А, А) представляет собой отношение «делит» между элементами множества А. Оно представлено графом на рисунке 7.

Это отношение обладает таким свойством: каждый элемент мно­жества А находится в этом отношении с самим собой, все пары типа (х, х)— (1, Г), (2, 2), (3, 3), (4, 4) —принадлежат гра­фику этого отношения. Это свойство отражается в графе (рис. 7) тем, что в каждой вершине графа имеется петля, указывающая на то, что каждая точка находится в этом отношении сама с собой. Отношение же «меньше» (рис. 6) не обладает этим свойством, более того, ни один элемент множества не находится в. этом отно­шении «меньше» с самим собой (ни одно число не меньше са­мого -себя). Ни в одной вершине этих графов нет петли.

Свойство отношения р = (Р, А, А),- состоящее в том, что хрх для всякой пары (х, х)£А² (или для всякого х£Л) называется рефлексивностью, а отношение р, обладающее этим свойством,— рефлексивным.

Свойство отношения р = (Р, А, А), состоящее в том, что хрх («х не находится в отношении р (х, х)») для всякой пары (х, х)£А² (или для всякого х£А) называется антирефлексивностью, а отно­шение р, обладающее этим свойством,—антирефлексивным¹.

Граф рефлексивного отношения характеризуется тем, что в каждой вершине имеется петля; граф антирефлексивного отношения — тем, что ни в одной верши­не нет петли, а граф отношения, не являющегося ни рефлексивным, ни антиреф­лексивным, может иметь в некоторых вершинах петли, в других — нет.

Среди перечисленных в § 2 отношений рефлексивными являются: «равно», «не меньше», «не больше», «делит», «делится на», «равенство и подобие фигур»; анти­рефлексивными являются отношения: «не­ равно», «меньше», «больше» между числами, «предшествует», «следует 'за» между точками прямой. Отношение «быть ро­весником» между людьми является ре­флексивным, отношение же «быть отцом»,
«бытьматерью», «быть братом», «быть сестрой», «выше», «старше», «моложе» — антирефлексивными. Отношение «быть другом» не является ни рефлексивным, ни антирефлексивным (бывают случаи, ког­да человек сам себе друг, и случаи, когда человек сам себе недруг).

2. Если a — b, то й = а, т. е. если пара (a, b) находится в от­ношении «равно», то и пара (Ь, а) находится в этом отношении.

Аналогичным свойством обладает и отношение «быть ровесни­ком»: если х ровесник у, то у ровесник х.

Если а<Ь, то ~16<а, т. е. если пара (а, Ь) находится в отно­шении «меньше» то пара (Ь, а) не находится в этом отношении.

Аналогично и отношение «старше»: если х старше у , то неверно, что у старше х.

Отношение «не больше» (меньше или равно: <!) обладает таким свойством: если х^у и у^х, то х = у.

Свойство отношения р = (Р, А, А), состоящее в том, что из хру следует урх для любой пары (х, у)£А², называется симметрич­ностью, а отношение р, обладающее этим свойством,— симметрич­ным.

Свойство отношения р, состоящее в том, что из хру следует ~\урх для любой пары (х, у)£А², называется асимметрия-ност ь ю, а отношение р, обладающее этим свойством,— асим­метричным. Свойство отношения р, состоящее в том, что из хру и урх следует х — у для любой пары (х, у)^А², называется антисимметричностью, а отношение р, обладающее этим свойством,— антисимметричным.

Граф симметричного отношения характеризуется тем, что любые две его вершины либо не связаны стрелкой, либо связаны двумя противоположно направленными стрелками; граф асимметричного (или антисимметричного) отношения — тем, что любые две его различные вершины связаны не более чем одной стрелкой1.

3. Несложно установить истинность следующих утверждений:

если х<у и y<z, то x<z;

если х = у и y — z, то x = z;

если х ровесник у и у ровесник z, то х ровесник z;

если л: старше у а у старше г, то х старше z; если a||b и Ь\\с, то а\\с.

однако если х — отец ужу — отец z, то х не есть отец z (а дедуш­ка); если х — друг у и у — друг z, то вообще не известно, является ли х другом z.

Свойство отношения р=(Р, А, А), состоящее в том, что из хру и ypz слеует xpz для любых х, у, z£A, называется тран­зитивностью, а отношение р, обладающее этим свойством,— транзи­тивным.

Свойство отношения р, состоящее в том, что из хру и ypz следует ~Лхрг для любых х, у, z£A, называется антитранзитивностью, а отношение р, обладающее этим свойством,— антитранзи­тивным.

Так, отношения «меньше», «равно», «быть ровесником», «старше;», «параллельно» являются транзитивными. Отношение «быть отцом» является антитранзитивным, а отношение «быть другом» не являет­ся ни транзитивным, ни антитранзитивным.