Отношения между двумя множествами

С целью уточнения вернемся к вопросу об отношении вклю-^ чения одного множества в другое.

Вообще говоря, в математике различают два вида включения: а) в широком смысле (нестрогое включение) и б) в узком смысле (строгое включение). Первое обозначается знаком £. Запись «Л £В» означает, что все элементы Л принадлежат В. При этом возможны два случая:

ai) все элементы В принадлежат Л, т. е. Л=В и В^А. В этом случае множества А и В состоят из одних и тех же эле­ментов и называются равными, что обозначается так: «Л=В». Например, если А — множество всех больших блоков, а В — множе­ство всех блоков, которые не являются малыми, то А = В. Как видно, равные множества по существу совпадают (при задании их перечислением элементов они могут отличаться лишь поряд­ком перечисления, который несуществен);

аг) не все элементы В принадлежат А, т. е. ЛеВ, но В^А. В таком случае говорят также, что А строго включается в В, или А является собственной (Или правильной) частью В. Это отношение в математической литературе обычно обозначает­ся символом «с» (АаВ).

В предматематической подготовке дошкольников встречается лишь строгое включение, собственная часть множества. Представ­ление о том, что все множество есть несобственная часть самого себя, противоречило бы житейскому опыту. Конечно, никакие спе­циальные обозначения здесь не применяются.

В играх с обручами моделируются и другие отношения, в ко­торых могут находиться два множества. Так например, множества красных (Л) и некрасных (Л) блоков не имеют ни одного общего элемента, т. е. их пересечение пусто (Л ПЛ= 0). Такие два мно-' жества, как мы уже знаем, называются непересекающими­ся (в литературе встречается и термин «дизъюнктные» множества). Множества красных (Л) и квадратных (В) блоков имеют общие элементы (красные квадраты), т. е. их пересечение непусто (ЛПВ^=0), Причем ни одно из этих множеств не включается в другое, т. е. не является подмножеством другого. Такие два множества называются пересекающимися.

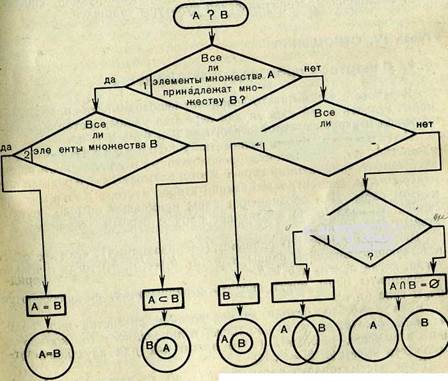
Таким образом, два произвольных множества Л и В могут находиться в одном из пяти отношений, которое можно выявить с помощью последовательности вопросов, представленных на ри­сунке 4. Каждый из этих вопросов требует ответа «да» или «нет» Подобные вопросы, касающиеся конкретных множеств предметов (без названия отношений между множествами), ставятся и перед дошкольниками с целью выявления отношений между множествами окружающих нас предметов. Например, вопрос «Все ли березы — деревья?» получает ответ «да», а вопрос «Все ли деревья — бере­зы?» — ответ «нет» (нужно добиваться обоснования этого ответа: «Имеются и другие деревья, не являющиеся березами, например дубы, тополя, липы, сосны...»). Этими вопросами и выявляется отно­шение включения между множествами берез и деревьев (разумеется, термином «включение» при этом не пользуются). Другой пример: «Все ли автомашины красные?» (Нет.) «Все ли красные пред­меты — автомашины?» (Нет, есть красные флаги, цветы и другие предметы красного цвета.) «Но имеются ли красные автомашины?» (Да.) Этими вопросами выявляется отношение пересечения между множествами красных предметов и автомашин.

Выявление правильных отношений между множествами окружаю­щих нас предметов — составная часть формирования и развития представлений дошкольников об окружающем мире. Выработка у дошкольников простейших представлений классификации окружаю­щих предметов является основой для формирования в дальней­шем математического мышления, связанного с моделированием и исследованием различных математических конструкций, способст­вует повышению алгоритмической культуры учащихся.

Гиава IV. ОТНОШЕНИЯ