Разбиение множества на классы
Разбиение множества на классы лежит в основе классифицирующей деятельности.
Обратимся еще раз к диаграмме, изображенной на_рисунке 1. Здесь имеем множество М и два его подмножества А и А, удовлетворяющие следующим условиям:_
1) каждое из множеств А я А непустое, т. е. АФ0 и АФ0;
2) они не пересекаются, т. е. А(]А=0;
3) их объединение образует множество М, т. е. А[]А — М.
Условия 1) —3) определяют разбиение множества М на два
класса (А и А).
Рассмотрим теперь диаграмму на рисунке 2.
Здесь имеем множество М и четыре подмножества: А(]В, Af]B, А О В, A f\ В. Обозначим их соответственно через К\, Kz, Кз, К*.
Нетрудно заметить, что выполняются условия, аналогичные
1)-3):
1) каждое из множеств Ki, Кг, Кз, К* непусто, т. е.
&Ф0, где i=l, 2, 3, 4;
2) эти множества попарно не пересекаются, т. е.
Ki(]Ki=0, где 1ф) и I, / = 1, 2, 3, 4;
3) их объединение образует множество М, т. е.
Объединение К\ U Ki U Кз U К* состоит из всех тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств К\, Кг, Д'з, К*.
В этом случае условия 1) —3) определяют разбиение мно'-' жества М на четыре класса.
Рассмотрим теперь игру с тремя обручами.
| чёрный обруч |
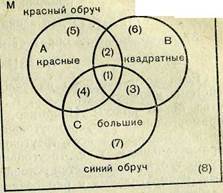
Пусть имеем три разноцветных (например, красный, черный и синий) обруча так, как показано на рисунке 3.
| Рис. 3. |
После того как образовавшиеся области (1) — (8) соот-ветствующим образом названы (внутри всех трех обручей, внутри красного и черного, но вне синего и т. д.), решается более сложная, чем в игре с двумя обручами, задача классификации блоков (или фигур) по трем свойствам. Предлагается расположить блоки, например, так, чтобы внутри красного обруча оказались все красные блоки, внутри черного — все квадратные, а внутри синего — все большие. После выполнения задачи расположения блоков ставятся восемь стандартных для любого варианта игры с тремя обручами вопросов. Какие блоки лежат: 1) внутри всех трех обручей; 2) внутри красного и черного, но вне синего обруча; 3) внутри черного и синего, но вне красного обруча; 4) внутри красного и синего, но вне черного обруча; 5) внутри красного, но вне черного и вне синего обруча; 6) внутри черного, но вне синего и вне красного обруча; 7) внутри синего, но вне красного и вне черного обруча; 8) вне всех трех обручей?
Как видно из рисунка 3, в игре с тремя обручами моделируется разбиение множества на восемь классов с помощью т£ех свойств:
И здесь также выполняются условия 1) —3):
1) каждое из множеств К\, Кг,-.-, Кг непустое, т. е.
К.Ф0, где /=1, 2, 3, ..., 8;
2) эти множества попарно не пересекаются, т. е.
Ki П К,= 0, где 1Ф\ и I, /=1, 2, 3, ..., 8;
3) их объединение образует множество М, т. е.
KiU^2U-UK8==Al.
Теперь можно ответить в самом общем виде на вопрос: что такое разбиение множества на классы?
Система множеств К\, Кг,--, Кп называется разбиением множества М на классы, а сами эти множества — к л а с-сами разбиения, если удовлетворяются следующие условия:
| I, 2, 3, ..., п; |
| где |
 1) каждое из множеств К\, Кг,---, Кп непустое, т. е.
1) каждое из множеств К\, Кг,---, Кп непустое, т. е.
2) эти множества попарно непересекающиеся, т. е.
ft,, fi Kj= 0 для всяких 1ф) и /, /= 1, 2, 3,...,п;
3) их объединение образует множество М, т. е.
Если хотя бы одно из условий 1) —3) не выполняется, то система множеств К\, /Сг,..., Кп не является разбиением множества М на классы. Например, система множеств косоугольных, прямоугольных и двупрямоугольных треугольников не образует разбиение множества всех треугольников, так как множество «двупрямоугольных», т. е. треугольников, содержащих по два угла, пусто, т. е. не выполняется условие 1). Система множеств косоугольных, прямоугольных и равнобедренных треугольников не образует разбиение множества всех треугольников, так как не выполняется условие 2); множества прямоугольных и равнобедренных треугольников пересекаются (существуют прямоугольные равнобедренные треугольники). Система множеств остроугольных и прямоугольных треугольников не образует разбиения множества треугольников, так как не выполняется условие 3) — объединение множеств остроугольных и прямоугольных треугольников не образует множество всех треугольников.
Дата добавления: 2015-07-10; просмотров: 1397;
