Подмножество. Дополнение множества и отрицание предложения
Рассмотрим теперь некоторое свойство, которым могут обладать или не обладать элементы нашего универсального множества.
Свойство «быть красным» выделяет из универсального множества подмножество красных блоков или фигур. Свойство «быть круглым» выделяет из этого множества другое подмножество—круглых блоков (или фигур).
Термин «подмножество» применяется в математике в смысле «часть множества». При этом, однако, не исключаются два крайних случая: когда часть множества (подмножество) совпадает со всем множеством, т. е. все элементы множества обладают рассматриваемым свойством, и когда эта часть не содержит ни одного элемента, например ни один блок не обладает свойством «быть зеленым». В последнем случае эту часть называют пустым множеством и обозначают символом «0».
Эти крайние случаи тоже можно смоделировать конкретными ситуациями, создаваемыми с помощью блоков (или фигур). Если, например, рассматривая только красные блоки (теперь множество красных блоков является универсальным), мы предлагаем выделить из них те, которые являются красными, то выделенное подмножество совпадает со всем рассматриваемым множеством. Если же предлагается из этих блоков отделить (переложить в другой ящик) все те, которые являются синими, то этот ящик останется пустым, т. е. фактич«ски в множестве красных блоков выделено «пустое множество» блоков.
Пусть множество М — некоторое универсальное множество, множество А — некоторое подмножество множества М. Символически это обозначается «.А &М». Говорят также, что множество А включается в М. Это означает, что все элементы множества А являются также элементами множества М. Выделение подмножества с помощью некоторого свойства может быть смоделировано с помощью игры с одним обручем. Опишем эту игру.
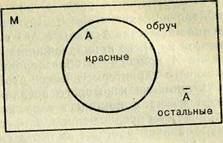
На полу (или на столе) располагают обруч (такой, который используется в художественной гимнастике, или поменьше). У каждого ребенка в руке один блок. Дети по очереди располагают блоки в соответствии с заданием воспитателя, например внутри обруча — все красные, а вне обруча — все остальные (рис. 1)
Эта задача, как правило, не вызывает затруднений у детей, уже различающих блоки по цвету и понимающих, что значит внутри и вне обруча. После решения задачи предлагаются два вопроса: «Какие блоки лежат внутри обруча?» и «Какие блоки лежат вне обруча?». Первый вопрос несложен для детей, так как
|
| Рис. 1. |
ответ содержится в условии уже решенной задачи. Второй вопрос на первых порах вызывает затруднения, так как в условии задачи говорится «все остальные», здесь же спрашивается «какие?»- Ответ, который мы хотим получить («Вне обруча лежат все некрасные блоки»), появляется не сразу. Такой ответ, как: «Вне обруча лежат все желтые и все синие блоки», по существу правильный. Но мы хотим выразить свойство блоков, оказавшихся вне обруча, как отрицание свойства тех, которые лежат внутри. Можно предложить детям назвать свойство всех блоков, лежащих вне обруча, с помощью одного слова, используя при этом слово «красные». Некоторые дети догадываются, и в дальнейшем, при проведений этой игры в различных вариантах, эти трудности уже не возникают.
В ходе этой игры отрабатывается переход от выражения некоторого свойства к выражению отрицания этого свойства:
внутри обруча вне обруча и т. п.
| некрасные неквадратные небольшие (малые) нетолстые (тонкие) круглые желтые |
| красные квадратные большие толстые некруглые нежелтые и т. п. |
Отвлечемся теперь от описанной конкретной игры и рассмотрим рисунок 1 как изображение некоторого множества М (с помощью множества точек внутри прямоугольника) и некоторого подмножества А (с помощью множества точек круга), выделенного из М некоторым свойством Р, т. е. Л = {*£М|Р (х)}. Оставшиеся элементы М, т. е. те, которые не принадлежат А, не обладают свойством Р. Множество всех этих элементов (тоже подмножество М) называется дополнением множества А (до универсального множества М) и обозначается через А (А с чертой). Если множество А характеризуется свойством Р, то его дополнение А характеризуется свойством не Р (если элементы А красные, то элементы А некрасные). Отрицание предложения Р (х), т. е. предложение « не обладает свойством Р», или «неверно, что х обладает свойством Р», обозначается символом «ПР(л:)». Таким образом, А—[х£М\~\Р{х)\,
т. е. множество А представляет собой множество всех х_из М, не обладающих свойством Р. Другое определение множества А (дополнения множества А : А ={х 6 М \ х £ А}, т. е. Л — множество всех элементов из М, не принадлежащих А. Как видно, образование дополнения А приводит к образованию отрицания предложения, выражающего характеристическое свойство множества А.
Отрицание некоторого предложения Р конструируется на русском языке с помощью слов неверно, что, поставленных перед отрицаемым предложением, или, если Р — простое предложение, использованием частицы не перед сказуемым.
Каждое предложение (имеется в виду высказывание или предикат) может быть истинным или ложным (предикат обращается в истинное или ложное высказывание при подстановке значений-вместо переменных). Истину обозначим через И, ложь — через Л. И и Л будем называть истинностными значе ни я м и предложений.
Если предложение Р истинно, то его отрицание IP ложно, если же Р ложно, то его отрицание IP истинно. Эта связь между истинностными значениями и определяет отрицание. Она может быть записана в виде следующей таблицы, называемой истинностной таблицей (или таблицей истинности):
Дата добавления: 2015-07-10; просмотров: 1978;
