Бинарные отношения. Под бинарным отношением понимают отношение между двумя предметами
Под бинарным отношением понимают отношение между двумя предметами. Дальше, говоря «отношение», будем иметь в виду .бинарное отношение. Выясним, что интуитивно понимают под отношением и как это понятие можно описать математически Из курса школьной математики известны многочисленные примеры отношений:
между числами: «равно», «неравно», «меньше», «больше», «неменьше», «не больше», «делит», «делится на»;между точками прямой: «предшествует», «следует за»;между прямыми: «параллельны», «пересекаются», «перпендикулярны», «скрещиваются»;между прямой и плоскостью: «параллельны», «пересекаются»,«перпендикулярны»;между плоскостями: «параллельны», «пересекаются», «перпендикулярны»;
— между геометрическими фигурами: «равно», «подобно» и др. Это, разумеется, далеко не полный перечень встречающихся в школьной математике отношений.
Примеры бинарных отношений встречаются не только в математике, но и всюду в жизни, вокруг нас. Родственные и другие отношения между людьми (быть отцом, дедушкой, матерью, бабушкой, братом, сестрой, другом, ровесником, старше, моложе, выше, ниже и др.) выступают как бинарные отношения. Отношения между событиями во времени (раньше, позже, одновременно), между предметами по их расположению в пространстве (выше, ниже, левее, правее, севернее, южнее и др.) также выступают как бинарные отношения.
Проанализируем складывающееся на базе опыта интуитивное понятие отношения. Прежде всего рассмотрим несколько примеров.
Пример 1. Возьмем отношение Р: «город х стоит на берегу реки у».
Всегда, когда говорим о каком-то отношении, мы имеем в виду множества предметов, между которыми установлено это отношение. В нашем примере имеется в виду некоторое множество А городов и некоторое множество В рек.
Пусть А ={Астрахань, Волгоград, Киев, Минск, Могилев, Москва, Ростов, Ульяновск} и В = {Волга, Днепр, Дон, Москва-река}.
Рассматриваемое отношение может быть задано следующей таблицей истинности:
| А | В | |||
| Волга | Днепр | Дои | Москва-река | |
| Астрахань | И | Л | л | л |
| Волгоград | и | л | л | л |
| Киев | л | и | л | л |
| Минск | л | л | л | л |
| Могилев | л | и | л | л |
В приведенной таблице буква И (истинно) поставлена в тех клетках, которые соответствуют парам (город, река,) находящимся в заданном отношении, т. е. если в предложении «город х стоит на берегу реки у» вместо х и у подставить имена соответствующих городов и рек, получим истинные высказывания («Астрахань стоит на берегу Волги», «Волгоград стоит на берегу Волги», «Киев стоит на берегу Днепра» и т. д.). Буква Л (ложно) стоит в тех клетках, которые соответствуют парам (город, река), не находящимся в данном отношении. Например, «Минск стоит на берегу Волги», «Могилев стоит на берегу Дона» и др.— ложные высказывания. Эта таблица дает ответ на вопрос: какой город из множества А стоит на берегу какой реки из множества В? Ответ можно записать и в виде множества пар:
{(Астрахань, Волга), (Волгоград, Волга), (Киев, Днепр), (Могилев, Днепр), (Москва, Москва-река), (Ростов, Дон), (Ульяновск,
Волга)}.
Сколько всего возможно пар вида (город, река), т. е. элементов декартова произведения АХ.В в данном примере? В таблице всего клеток (или пар) 32. Таким образом, рассматриваемое отношение может быть задано с помощью множества из 7 пар, представляющего собой подмножество декартова произведения
АХ В.
|
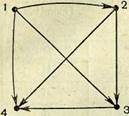
Данное отношение можно задать и более наглядным способом — с помощью фигуры, называемой ориентированным графом, состоящей из точек, вершин графа и стрелок, ребер графа.
На рисунке 6 изображен граф, задающий отношение «меньше» в множестве А;
элементы множества А изображены вершинами графа, а стрелка исходит из вершины а и направлена к вершине b, если предложение a<b истинно.
Рассмотренные примеры 1 и 2 показывают, что всегда, когда речь идет о некотором отношении, имеются в виду два множества Л и В (эти множества могут, в частности, совпадать, как в примере 2, т. е. возможно, что В = А) и при этом некоторые элементы множества А находятся в данном отношении с некоторыми элементами множества В или того же множества А. Таким образом, всякое отношение между элементами множеств А и В (или между элементами множества А) порождает множество пар, первые компоненты которых принадлежат А, вторые В (или тоже А), т. е. порождает подмножество АХВ (или АХА), причем такое, что элементы каждой пары и только они находятся в данном отношении.
Как видно из проведенного анализа интуитивного понятия отношения, всякое отношение между элементами двух множеств А и В полностью характеризуется тремя множествами: А и В, между элементами которых установлено отношение, некоторым множеством пар Р — подмножеством АХВ, т. е. декартовым произведением. Один из путей определения математического понятия отношения и состоит в отождествлении этого понятия с указанной тройкой множеств. Если же определяют отношение вообще, без указания, между элементами каких множеств оно установлено, то обычно отождествляют его с множеством пар Р.
Отношением между элементами непустых множеств А и В называется тройка множеств
р=(Р, А, В), где Рс=АхВ.
Множество пар Р называется графиком отношения р. Об элементах пары (je, у), принадлежащей графику Р, говорят, что они находятся в отношении р, и записывают это так: «хру»
Таким образом, записи «(*, у)£Р» и «.хру» равносильны. Если В —А, то р=(Р, А, А) называется отношением между элементами множества А. Так, в примере 2 мы имели отношение «меньше» между элементами множества А — {\, 2, 3, 4}.
Дата добавления: 2015-07-10; просмотров: 2535;
