Отсчета

Одну из произвольно выбранных инерциальных систем отсчета "К" будем условно считать неподвижной. Движение материальной точки относительно неподвижной системы отсчета называют абсолютным движением. Уравнение второго закона Ньютона, записанное в этой системе отсчета имеет вид:

,

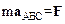здесь m – масса материальной точки, a_АБС – ее ускорение относительно неподвижной ИСО, F – равнодействующая всех приложенных к материальной точке сил.

Предположим, что система К* (см. рис. 8.1) движется относительно системыК со скоростью V_ПЕР, с ускорением а_ПЕР и вращается с угловой скоростью w относительно оси NN, проходящей через начало координат системы К*. Система К*, очевидно, не является инерциальной. Движение этой системы отсчета относительно неподвижной инерциальной системы отсчета К называют переносным движением, соответствующие физические характеристики движения будем выделять индексами "пер" – "переносные". Соответствующие величины, измеряемые в движущейся системе К*, назовем относительнымии будем отмечать их знаком (*).

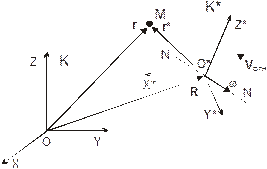
Рис. 8.1. Взаимное расположение инерциальной К и неинерциальной К* систем отсчета

Пусть движущаяся материальная точка М имеет в К* координаты X*, Y* и Z* и ее радиус-вектор равен

,

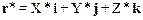в системе К радиус-вектор точки М есть вектор

.

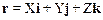Обозначим также через R радиус-вектор начала координат подвижной системы К* относительно системы К. Из рисунка 8.1 видно, что радиус-векторы точки М связаны между собой следующим образом:

.

Дифференцируя соотношение (8.2) по времени получим

.

.

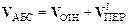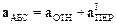В последних соотношениях введены следующие обозначения: V_АБС=dr/dt и а_АБС=d²r/dt² абсолютные скорость и ускорение материальной точки М в неподвижной СО К; V_ОТН=dr*/dt и а_ОТН=d²r*/dt² –скорость и ускорение точки М относительно подвижной СО К*, первая и вторая производные от R определяют линейные переносные скоростьV¢_ПЕР и ускорениеа¢_ПЕР начала подвижной – неинерциальной системы отсчета "К*" относительно ИСО "К".

Очевидно, что уравнение (8.3) выражает классический закон сложения скоростей, уравнение (8.4) показывает, что абсолютное ускорение а_АБС материальной точки относительно ИСО равно векторной сумме ее относительного а* и переносного а¢_ПЕР ускорений.

Вычислим относительную скоростьчастицы в системе К*. По определению скорости

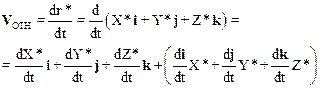
Первое слагаемое в полученном соотношении представляет собой относительную скорость частицы в подвижной СО – V*. Второе слагаемое преобразуем с учетом того (см. ), что производные векторов постоянной длины (например, ортов i, j, k) вращающихся вместе с системой координат с угловой скоростью w равны

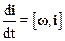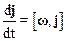, и .

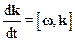Можно записать:

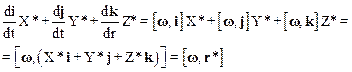
Окончательно для относительной скорости V_ОТН имеем:

.

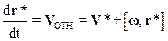Выражение (8.3) для абсолютной скорости V_АБС принимает вид

.

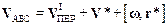В формуле (8.5) 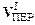представляет скорость, которую имела бы в системе К материальная точка, неподвижная в системе К*; эта скорость совпадает с линейной скоростью начала подвижной системы К*. Слагаемое [w,r*] – линейная переносная скорость точки, вызванная вращением К*. Таким образом, переносная относительно К скорость точки М равна:

,

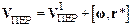а абсолютная скорость, соответственно, равна:

.

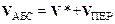Заметим, что переносную скорость 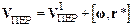имела бы неподвижная в системе К* материальная точка за счет поступательного движения начала системы отсчета К* и за счет ее вращения.

Величину абсолютного ускорениянайдем дифференцированием (8.6) по времени.

.

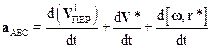Рассмотрим последовательно слагаемые, входящие в (8.9). Первое слагаемое равно ускорению а₀ начала подвижной системы отсчета по отношению к неподвижной. Производная d[w,r*]/dt равна

.

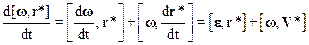Преобразуем последний член выражения (8.10) с помощью соотношения (8.5):

.

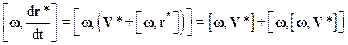Производная по времени от V*, подобно производной r*, равна

.

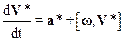Подставляя выражения для производных в (8.9) приходим к выражению:

,

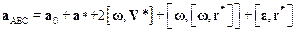или:

.

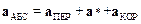В последнем соотношении а_ПЕР – переносное ускорение, определяемое только характером движения начала координат подвижной СО относительно неподвижной:

,

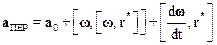где а₀ – ускорение поступательного движения начала координат системы К*, dw/dt=e – ее угловое ускорение. Переносное ускорение представляет собой ускорение материальной точки, покоящейся в системе К*. Слагаемое [dw/dt,r] – вызвано неравномерным вращением СО, и при w=const обращается в ноль. Относительное ускорение а_ОТН равно производной dV*/dt.

Последний член в (8.13) а_КОР – кориолисово ускорение; оно зависит как от относительного, так и переносного движения

.

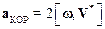Укажем, что формула (8.13) представляет математическое выражение теоремы Кориолиса:

· абсолютное ускорение представляет собой векторную сумму относительного, переносного и кориолисова ускорений.

Выражение [w,[w,r]], как было показано ранее, (см. (1.23)), определяет центростремительное ускорение, направленное к оси вращения.