Колебательного движения

При движении материальной точки в реальных условиях возникает сила сопротивления, которая при малых скоростях может, в некотором приближении, считаться прямо пропорциональной первой степени скорости точки: F_ТР = rV, где r – постоянный коэффициент.

В зависимости от коэффициента сопротивления различают три вида затухающих колебательных движений:

А. Случай малого сопротивления (b = r/2m < w₀).

Этот случай подробно рассмотрен выше. Было установлено, что пружинный маятник с трением совершает затухающие колебания, подчиняющиеся следующему закону:

.

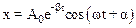Колебания, описываемые формулой (7.23), строго говоря, не является гармоническим, так как их амплитуда 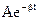монотонно убывает со временем. По аналогии со свободными гармоническими колебаниями можно ввести понятия о круговой частоте (см. (7.24)), периоде (7.26) и амплитуде (7.25) таких колебаний.

В.Случай большого сопротивления (b > w₀).

Анализ влияния сопротивления в этом (и следующем разделе С) проведем качественно. Общее решение уравнения (7.22) не содержит функции синуса или косинуса. Система движется согласно уравнению:

.

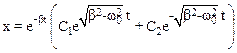Благодаря экспоненциальному множителю колебание быстро затухает (при t®¥ имеем x®0). Характер движения зависит от начальных условий. При х₀ ³0 и V₀>0, т. е. когда в начальный момент материальная точка смещена из положения статического равновесия в направлении оси х, и ей сообщена начальная скорость в том же направлении, материальная точка вначале отклоняется в указанном направлении (рис. 7.6, кривая I), а затем асимптотически приближается к положению равновесия (не переходя через него). При х₀ >0 и V₀<0 (и 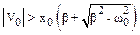), то есть, когда в начальный момент материальная точка смещена из положения статического равновесия на х₀,и ей сообщена противоположно направленная скорость, модуль которой удовлетворяет указанному выше неравенству, материальная точка приближается к положению равновесия, проходит его (рис. 7.6, кривая 2) и отклоняется в противоположную сторону и затем асимптотически приближается к положению равновесия (больше не переходя через него).

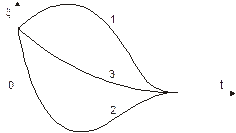
Рис. 7.6. Апериодические колебания

При х₀ >0 и V₀<0 (и 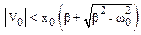), т. е. когда в начальный момент материальная точка смещена из положения равновесия в положительном направлении оси и отпущена без начальной скорости либо ей сообщена в противоположном направлении начальная скорость, модуль которой удовлетворяет указанному неравенству, материальная точка асимптотически приближается к положению равновесия, не переходя через него (кривая 3, на рис. 7.6).

С. Предельный случай (b = k).

Материальная точка совершает апериодическое движение в соответствии с уравнением

.

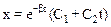При t ® ¥ смещение х становится неопределенным: 0×¥. Раскрытие неопределенности по правилу Лопиталя указывает, что 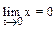, что говорит о затухании движения.

Характер затухания зависит от начальных условий движения. При х₀³ 0 и V₀>0 движение маятника соответствует кривой 1 на рисунке 7.6. При х₀ >0 и V₀<0(при 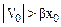) движение соответствует кривой 2. При x₀>0 и V₀<0 (причем |х₀|<bх₀) движение соответствует кривой 3.