Затухающие колебания. Во всякой реальной колебательной системе имеются силы трения, которые принципиально меняют характер колебательного процесса

Во всякой реальной колебательной системе имеются силы трения, которые принципиально меняют характер колебательного процесса. Диссипация энергии приводит к тому, что амплитуда колебаний уменьшается с течением времени. Рассмотрим колебания пружинного маятника, подверженного воздействию силы тяжести mg, силы упругости F_УПР и силы вязкого трения F_ТР, существующей при движении в газе или жидкости. В этих средах при небольших скоростях колеблющегося тела сила трения пропорциональна скорости и антипараллельна ей: F_ТР = –rV, здесь r – коэффициент сопротивления.

На рисунке 7.4А показано равновесное (статическое) положение маятника.

Рис. 7.4. А – состояние равновесия маятника, В – положение колеблющегося маятника в некоторый момент времени

Запишем условие равновесия:

.

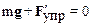Уравнение второго закона Ньютона для колеблющегося маятника с вязким трением имеет вид:

.

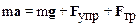Уравнения состояний А и В образуют систему

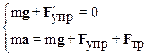(7.20)

Направим ось x вдоль пружины по вертикали вниз, взяв начало отсчёта в положении статического равновесия груза m. Предположим, что груз движется в сторону возрастания х. Сила трения F_ТР направлена противоположно скорости движения груза, т. е. вертикально вверх. Проецируя уравнения системы (7.20) на ось х, получим:

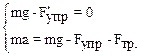
Подставив в эти уравнения дополнительные соотношения

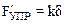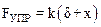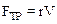, , , и используя определения скорости и ускорения, имеем:

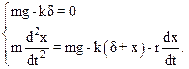
Вычитая первое уравнение из второго уравнения системы, получим закон движения пружинного маятника:

.

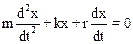Разделим все члены уравнения (7.20) на m и введем следующие обозначения:

, .

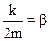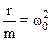Уравнение (7.20) приводится к виду

.

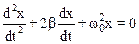Решение полученного дифференциального уравнения второго порядка с постоянными коэффициентами будем искать в виде функции 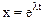. Составим для (7.21) характеристическое уравнение:

,

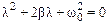корни которого равны

.

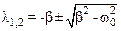При малом b, что обычно выполняется в колебательной системе, подкоренное выражение меньше нуля, поэтому формулу для l можно преобразовать следующим образом:

,

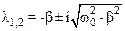здесь i – мнимая единица.

Уравнение движения груза (7.21) имеет два решения 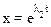. Общее решение уравнения, как известно из курса математического анализа имеет вид

,

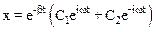где введены обозначения: 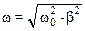, С₁ и С₂ – некоторые постоянные.

Используя формулу Эйлера, общее решение (7.23) преобразуем к виду:

,

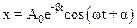где A₀ и a – постоянные.

Движение маятника, описываемое уравнением (7.23), можно рассматривать как гармоническое с циклической частотой

,

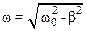и амплитудой, зависящей от времени:

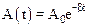
Графическое изображение зависимости колеблющейся величины от времени дано на рисунке.

Период колебаний Т_С маятника с трением равен

.

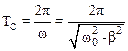· В присутствии сил сопротивления периодколебаний увеличивается по сравнению с периодом собственных колебаний.

Амплитуда колебаний (см. 7.25) убывает со временем по экспоненциальному закону.

Допустим, что в момент времени t_i амплитуда колебаний равна А_i. Следующее отклонение А_i+1 в том же направлении будет иметь место через период: т. е. если

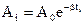, то , …

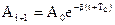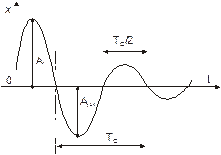
Рис. 7.5. Затухающие колебания смещения Х

· Декрементзатухания – величина, равная отношению двух последовательных амплитуд.

Декремент затухания D, показывает во сколько раз уменьшилась амплитуда за время, равное одному периоду колебаний. Вычислим величину декремента, для чего найдем отношение амплитуд двух последовательных колебаний:

.

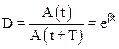· Логарифмическийдекрементзатухания l – скалярная величина, равная логарифму декремента затухания:

.

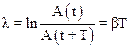Используя величину декремента b, закон изменения амплитуды (7.25) можно записать так:

.

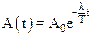За время t, в течение которого амплитуда уменьшится в е раз (е – основание натуральных логарифмов), маятник совершит N = t/T колебаний. Из соотношения

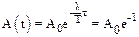
следует 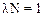, или .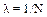

Таким образом, логарифмический декремент затухания есть величина, обратная числу колебаний, в результате которых амплитуда уменьшается в е раз.