Вынужденные колебания. · Вынужденныеколебания– это колебания, происходящие в системе при воздействии на нее периодической силы.

· Вынужденныеколебания– это колебания, происходящие в системе при воздействии на нее периодической силы.

Рассмотрим колебания системы, подверженной воздействию силы тяжести mg, силы упругости F_УПР, внешней периодической силы F= F₀coswt. Во избежание решений, обращающихся в бесконечность, будем учитывать силу вязкого трения F_ТР = – rV, всегда присутствующую при движении в газе или жидкости.

Уравнение второго закона Ньютона для колеблющегося маятника с вязким трением имеет вид:

.

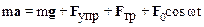Рассуждения, аналогичные проведенным в предыдущем разделе, приводят в одномерном случае к дифференциальному уравнению:

,

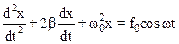где введены следующие обозначения: m – масса колеблющегося тела, k – коэффициент упругости пружины, r – коэффициент сопротивления, f₀=F₀/m и, наконец,

, .

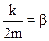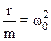Решение дифференциального уравнения (7.33), которое представляет собой уравнение второго порядка с постоянными коэффициентами, неоднородное, представляет собой сумму общего решения х₁ однородного уравнения

,

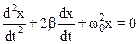и какого-нибудь частного решения х₂ неоднородного уравнения (7.33).

Общее решение уравнения (7.34), представляющего собой уравнение колебаний в системе с трением, найдено в предыдущем разделе:

,

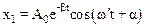где 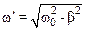, А₀ и a – некоторые постоянные.

Частное решение уравнения (7.33) имеет следующий вид:

.

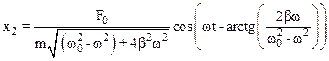Обратим внимание на то, что решение х₁ за счет множителя e ^–bt экспоненциально затухает со временем. Оно описывает колебания на их начальной стадии и соответствует времени установления колебаний, в нем присутствует частота собственных колебаний маятника с трением: .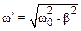

Частное решение – х₂ – зависит от частоты w₀ свободных колебаний и частоты w вынуждающей силы. Временная зависимость интенсивности вынужденных колебаний графически представлена на рисунке (7.7).

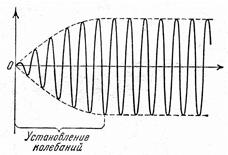
Рис. 7.7. Амплитуда вынужденных колебаний в зависимости от времени