В неинерциальной системе отсчета
В уравнение (8.1) второго закона динамики Ньютона подставим соотношение (8.13) и перепишем его следующим образом:
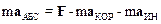 .
.
Формула (8.16) показывает, что к реальной силе F, действующей на материальную точку m, добавились две силы инерции:
силаКориолиса
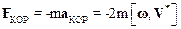
и переносная силаинерции
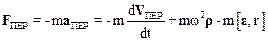 ,
,
где r – составляющая радиус-вектора движущейся точки перпендикулярная к оси вращения.
Силы инерции, в отличие от реальных сил, не вызваны взаимодействием материальной точки с каким-то реальными телами, а возникают благодаря ускоренному движению системы К*. очевидно, что силы инерции неинвариантны относительно преобразования координат и не удовлетворяют третьему закону Ньютона, но их воздействие эквивалентно воздействию силового (гравитационного) поля. Силы инерции всегда являются внешними по отношению к любой механической системе.
Как следует из (8.18) в общем случае переносная сила инерции состоит из трех слагаемых. Первое слагаемое – силаинерции связанная с ускоренным движением поступательным движением неинерциальной СО К*. Третье слагаемое вызвано неравномерным вращением подвижной системы отсчета. Наконец, сила, представленная вторым слагаемым mw2r, получила название центробежной силыинерции или короче – центробежной силы.
Рассмотрим проявление центробежной силы на следующем примере. Предположим (см. рис. 8.2), что на диске, который может вращаться вокруг вертикальной оси, расположена радиальная спица с одетой на нее бусинкой М, которая крепится упругой связью к центру диска. При увеличении угловой скорости связь растягивает до тех пор, пока упругая сила не обеспечит центростремительное ускорение аЦ=-mV2R/R2 (R – радиус-вектор бусинки). Очевидно, что в неинерциальной системе К*, связанной с диском, бусинка покоится. Выполнение условия равновесия можно объяснить тем, что во вращающейся системе на бусинку кроме силы упругости действует также уравновешивающая ее центробежная сила FЦ= mV2R/R2.
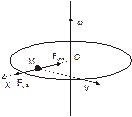
| Рис. 8.2. |
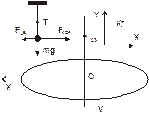
Рассмотрим теперь движение шарика, подвешенного на нити над вращающимся диском (см. рис. 8.3) с позиции наблюдателя из неподвижной инерциальной системы отсчета К, и с позиции наблюдателя из неинерциальной системы К*, жестко связанной с вращающимся диском.
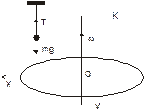 А А
|  В. Рис. 8.3. В. Рис. 8.3.
|
В системе К шарик покоится, что выражается уравнением T+mg=0. Относительно системы К* шарик движется с постоянной по величине скоростью по окружности с центростремительным ускорением aЦ= -V2R/R2, здесь R – радиус круговой траектории, V – линейная скорость тела. Уравнение движения шарика в системе К* (8.16) имеет вид:
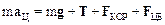 .
.
Проецируя на оси координат, получим систему уравнений:
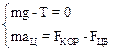
Вычислим (см. (8.15), (8.18)) силы, входящие во второе уравнение системы.
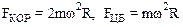 .
.
Подставляя найденные величины во второе уравнение системы, получим:
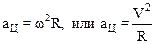 .
.
Отметим, что Кориолисова сила инерции возникает во вращающейся СО только тогда, когда материальная точка движется относительно этой системы. При условии, что относительная скорость тела VОТН равна нулю, сила Кориолиса также обращается в ноль. Подчеркнем еще раз (см. (8.17)), что сила Кориолиса действует перпендикулярно скорости относительного движения и не совершает работы, т. е. является гироскопической силой.
Заканчивая рассмотрение сил инерции отметим, что можно привести много примеров действия сил инерции в земных условиях. Они проявляют себя при взвешивании тел, вызывают отклонение падающих тел от направления отвеса, в баллистике требуют учета отклонения снарядов в зависимости от направления полета снаряда и т. д.
Влияние силы Кориолиса на движение тела в НИСО впервые продемонстрировал Ж. Фуко. Опыт, поставленный им в Парижской обсерватории, показал, что плоскость колебаний математического маятника поворачивается с течением времени относительно вертикальной оси. Расчетный период t вращения плоскости, которой колеблется маятник
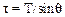
находится в хорошем соответствии с результатами наблюдений. В последней формуле введены следующие обозначения: Т – период вращение Земли относительно инерциальной (гелиоцентрической) системы отсчета, q – географическая широта местности. На рисунке 8.4 в качестве примера, показана траектория математического маятника в опыте Фуко, поставленном на северном полюсе Земли.

| Рис. 8.4. К опыту Фуко. Вид сверху на траекторию математического маятника |
Дата добавления: 2015-08-08; просмотров: 900;
