УравнениеБернулли

Уравнение Бернулли является основным уравнением, описывающим движение идеальной несжимаемой жидкости. С формальной точки зрения уравнение Бернулли выражает закон сохранения энергии для жидкости в трубке тока. Оно может быть использовано и для газа при условии, что его давление, а значит и объем, изменяются достаточно слабо, и можно пренебречь изменением плотности.

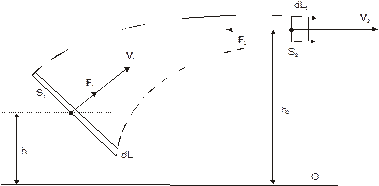
Выберем (см. рис. 9.4) в стационарно текущей жидкости трубку тока небольшого диаметра так, чтобы физические величины, используемые в дальнейшем, можно было бы считать постоянными. Предположим, что два ее поперечных сечения, ориентированных перпендикулярно линиям тока, находятся на различной высоте h₁ и h₂ над исходным (нулевым) уровнем и имеют площади S₁ и S₂; скорости течения жидкости в этих сечениях равны, соответственно, υ₁ и υ₂.

Пусть за время dt через сечение S₁ в трубку втекает объем жидкости dW₁=S₁dL₁, где dL₁= V₁dt. За это же время через сечение S₂ вытекает объем dW₂=S₂V₂dt. Из условия неразрывности струи следует: dW₁= dW₂. Движение жидкости в трубке тока выглядит так, как если бы элементарный объем жидкости dW₁ из положения I переместился в положение II.

Рис. 9.4. К выводу уравнения Бернулли

Найдем изменение DЕ полной механической энергии объема dW:

,

где:

.

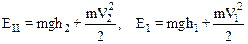В последнем соотношении m – масса жидкости, объем которой равен dW: m=rdW. Подставляя (9.3) в (9.2), получим:

.

Поскольку движение происходит в поле тяжести, трение отсутствует, а силы давления на боковую поверхность трубки тока работы не совершают, то изменение энергии объема жидкости вызвано только работой сил давления на основания трубки тока S₁ и S₂:

.

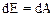Сила давления F₁ совершает за время dt элементарную работу по перемещению элементарного объема dW_I: dА₁=F₁dl₁=P₁S₁V₁dt. Аналогичным образом вычислим работу силы F₂ в сечении S₂. dA₂= – F₂dl₂= – F₂V₂dt. Работа силы F₂ отрицательна, так как направления вектора скорости V₂ и силы давления F₂ противоположны.

Результирующая работа сил давления, по перемещению жидкости равна:

.

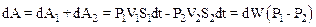Подставляя (9.4) и (9.6) в формулу (9.5) и перегруппировав члены, находим:

.

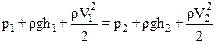Это и есть уравнениеБернулли. Поскольку выбор положений 1 и 2 сделан произвольно, то полученное соотношение имеет общий характер: величина

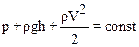
имеет одно и тоже значение в любом сечении трубки тока. Все члены в правой части уравнения имеют размерность давления и представляют собой статическое, гидростатическое и динамическое давления.

С помощью уравнения Бернулли легко получить некоторые важные результаты, как для движущейся жидкости, так и для жидкости, находящейся в равновесии.