Резонанс. · Резонансомназывают явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте собственных колебаний.

· Резонансомназывают явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте собственных колебаний.

· Вынуждающаясила – внешняя периодическая сила, действующая на колебательную систему.

· Резонансная частота – частота, при которой наступает явление резонанса.

Явление резонанса вызвано зависимостью (см. (7.35)) амплитуды установившихся вынужденных колебаний от частоты внешнего воздействия:

.

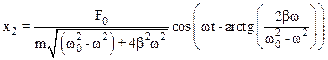Найдем резонансную частоту w_РЕЗ для пружинного маятника из условия максимума величины х₂. Очевидно, что х₂ принимает максимальное значение, если знаменатель выражения (7.35) принимает минимальное значение. Условие экстремума знаменателя записывают так:

.

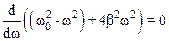Вычисляя производную, после преобразований получим выражение, позволяющее найти w_РЕЗ:

.

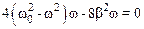Полученное уравнение имеет три корня:

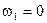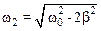, и .

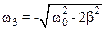Очевидно, что 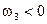не удовлетворяет условию, т. к. частота существенно положительная величина. При каком из корне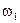й или 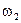выполняется условие минимума, выясним, определяя знак второй производной:

.

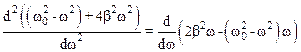При w₁=0 вторая производная отрицательна, что соответствует максимуму знаменателя и минимуму колеблющейся величины х₂. При w₂ знаменатель минимален, значитw₂=w_РЕЗ:

.

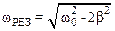Подставив значение w_РЕЗ в выражение (7.35), найдем выражение для резонанснойамплитуды А_РЕЗ:

.

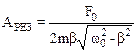Последнее соотношение указывает на отмеченную ранее необходимость учета сопротивления среды (b¹0), в противном случае резонансная амплитуда обращалась бы в бесконечность.

При w®0 выражение (7.38) принимает вид

,

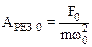или

,

что соответствует статическому растяжению пружины в соответствии с законом Гука.

При стремлении частоты вынуждающей силы к бесконечности амплитуда вынужденных колебаний стремится к нулю. Зависимость амплитуды от частоты в виде так называемой резонанснойкривой представлена на рисунке 7.8.

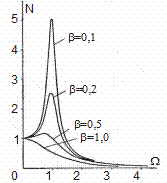
Рис. 7.8. Резонансная кривая. Зависимость отношения амплитуды вынужденных колебаний к величине статического смещения от безразмерной частоты W. Использованы относительные единицы: W = w/wP и N = A/AР

Из формулы (7.35) вытекает также, что фазы вынуждающей силы и вынужденных колебаний отличаются друг от друга: вынужденные колебания отстают по фазе от вынуждающей силы на величину

,

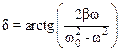заключенную в пределах от 0 до p (см. рис. 7.9).

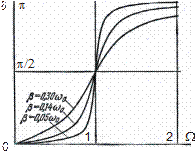
Рис. 7.9. Зависимость сдвига фаз d от относительной частоты W = w/wP при различных значениях b

Как видно из приведенного рисунка, при малой частоте вынуждающей силы и при малом затухании сдвиг фаз стремится к нулю, т. е. колебания по фазе совпадают с фазой вынуждающей силы; при высоких частотах сдвиг фаз составляет p – смещение и сила находятся в противофазе и, наконец, при резонансе сдвиг фаз близок к p/2.