Связь кинетической энергии тела с работой внешних, приложенных к телу (теорема о кинетической энергии).
Пусть на тело массы m, движущееся прямолинейно, действует постоянная сила, направление которой совпадает с направлением перемещения 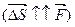 .Тело движется с пстоянным ускорением
.Тело движется с пстоянным ускорением 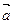 и га перемещении
и га перемещении 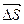 скорость тела возрастает от
скорость тела возрастает от 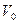 до
до 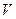 , т.е. кинетическая энергия возрастает от
, т.е. кинетическая энергия возрастает от 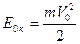 до
до 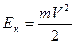 , работа силы
, работа силы 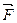 на перемещении
на перемещении 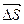 равна
равна 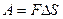 . Учитывая, что
. Учитывая, что 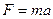 ,
, 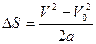 получим формулу
получим формулу
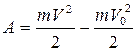 ,
,
которая устанавливает связь приращения кинетической энергии с работой внешних сил, приложенных к телу. Эта формула есть математическое выражение теоремы о кинетической энергии.
Итак, изменение кинетической энергии тела равно работе внешних сил, действующих на него:
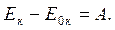
6. Силы потенциальные –силы, работа которых при перемещении материальной точки не зависит от формы траектории, но зависит от начального и конечного положения точки в пространстве.
Примером потенциальной силы является сила тяжести. Пусть тело массы m соскальзывает без трения по наклонной плоскости длиной l и высотой h (Рис.54).
 При свободном падении тела с высоты h, сила тяжести совершает работу
При свободном падении тела с высоты h, сила тяжести совершает работу 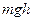 .При скольжении по наклонной плоскости сила
.При скольжении по наклонной плоскости сила 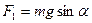 совершает работу
совершает работу  ,
, 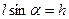 , т.е. работа силы
, т.е. работа силы 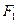 равна
равна 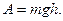 Сила
Сила 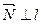 и работу не совершает.
и работу не совершает.
Итак, при движении по вертикали и по наклонной плоскости сила тяжести совершает одну и ту же работу 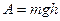 , которая зависит от высоты наклонной плоскости, но не зависит от угла наклона плоскости, т.е. не зависит от формы траектории.
, которая зависит от высоты наклонной плоскости, но не зависит от угла наклона плоскости, т.е. не зависит от формы траектории.
 Примером непонтенциальной силы является сила трения, которая зависит от пройденного пути, т.е. от формы траектории.
Примером непонтенциальной силы является сила трения, которая зависит от пройденного пути, т.е. от формы траектории.
7. Потенциальная энергия. Пусть по кривой поверхности под действием силы тяжести без трения скользит тело массы m (Рис.55)
Эту кривую поверхность можно рассматривать как ряд очень коротких наклонных плоскостей работа силы тяжести на каждой из них равна 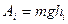 , где
, где  - высота
- высота 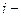 ой наклонной плоскости. Суммируя работу, произведённую силой тяжести на каждой из них и учитывая, что
ой наклонной плоскости. Суммируя работу, произведённую силой тяжести на каждой из них и учитывая, что 
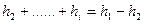 (Рис.55), получим работу силы тяжести при перемещении тела из точки A в точку В:
(Рис.55), получим работу силы тяжести при перемещении тела из точки A в точку В:
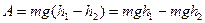 .
.
Итак, при переходе с высоты 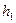 высоту
высоту 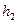 работа силы тяжести равна разности величин
работа силы тяжести равна разности величин  и
и 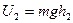 , т.е. никоим образом не зависит от траектории движения. Величина
, т.е. никоим образом не зависит от траектории движения. Величина 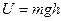 есть потенциальная энергия тела, находящегося на высоте h над поверхностью Земли. Потенциальная энергия тела на поверхности Земли равна нулю.
есть потенциальная энергия тела, находящегося на высоте h над поверхностью Земли. Потенциальная энергия тела на поверхности Земли равна нулю.
Таким образом, приходим к выводу, что работа потенциальной силы равна разности потенциальных энергий в начальном и конечном положениях:
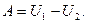

Из этого равенства следует, что работа потенциальной силы по замкнутому контуру равна нулю.
В каждой конкретной задаче всегда можно потенциальную энергию в какой либо точке пространства принять равной нулю. Например, потенциальную тела на поверхности Земли мы приняли равной нулю. Полагая  получим
получим  .
.
Таким образом, потенциальная энергия тела в данной точке пространства равна работе, совершаемой потенциальной силой, при перемещении тела из этой точки в точку, в которой потенциальная энергия принята равной нулю.
Ранее мы показали, что работа силы упругости 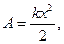 совершаемая силой упругости при деформации тела, зависит только от удлинения х деформируемого тела. Следовательно, сила упругости есть сила потенциальная. Принимая потенциальную энергию недеформированного тела равной нулю получим, что потенциальная энергия упруго деформированного тела равна работе, совершаемой при его деформации:
совершаемая силой упругости при деформации тела, зависит только от удлинения х деформируемого тела. Следовательно, сила упругости есть сила потенциальная. Принимая потенциальную энергию недеформированного тела равной нулю получим, что потенциальная энергия упруго деформированного тела равна работе, совершаемой при его деформации:
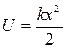 .
.
Итак, потенциальная энергия тела это энергия, обусловленная его взаимодействием с другими телами, либо взаимодействием между отдельными его частями, как в случае упругих сил.
Потенциальная энергия тела на некоторой высоте над поверхностью Земли обусловлена гравитационным взаимодействием тел и Земли. Потенциальная энергия упруго деформированного тела обусловлена электромагнитным взаимодействием между его молекулами.
Кроме этого потенциальная энергия в отличие от кинетической может быть и отрицательной в зависимости от выбора нуля отсчета.
Следует отметить, что часто работу потенциальной силы записывают как разность потенциальных энергий в конечном – 2 и в начальном – 1 положениях (состояниях) взятой с отрицательным знаком:
 .
.
8. Принцип минимума потенциальной энергии. Если при перемещении тела его потенциальная энергия уменьшается  то работа потенциальной силы положительна
то работа потенциальной силы положительна

 Следовательно угол между направлениями силы и перемещения острый и сила имеет
Следовательно угол между направлениями силы и перемещения острый и сила имеет  компоненту в направлении перемещения, т.е. в сторону убывания потенциальной энергии. Это свойство присуще всем типам потенциальных энергий. Поэтому любая замкнутая система стремится перейти в состояние с минимумом потенциальной энергии.
компоненту в направлении перемещения, т.е. в сторону убывания потенциальной энергии. Это свойство присуще всем типам потенциальных энергий. Поэтому любая замкнутая система стремится перейти в состояние с минимумом потенциальной энергии.
9. Три типа равновесия:
а) Устойчивое равновесие – положение, в котором потенциальная энергия тела минимальна. В этом случае при отклонении тела от положения равновесия потенциальная энергия тела взрастает и возникает сила, стремящаяся вернуть тело в положение равновесия (Рис. 56).
 б) Неустойчивое равновесие – равновесие, в котором тело, выведенное из положения равновесия, не возвращается в исходное положение. В этом случае при удалении от положения равновесия потенциальная энергия тела уменьшается и возникает сила, направленная в сторону от положения равновесия (Рис.57).
б) Неустойчивое равновесие – равновесие, в котором тело, выведенное из положения равновесия, не возвращается в исходное положение. В этом случае при удалении от положения равновесия потенциальная энергия тела уменьшается и возникает сила, направленная в сторону от положения равновесия (Рис.57).
в) безразличное равновесие – равновесие, при котором потенциальная энергия тела остается неизменной при его удалении от от первоначального положения (Рис, 58)
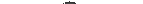 10 Полная механическая энергия системы – сумма её кинетической и потенциальной энергий
10 Полная механическая энергия системы – сумма её кинетической и потенциальной энергий
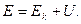
11. Закон изменения механической энергии. Согласно теореме о кинетической энергии изменение кинетической энергии равно работе вех сил, действующих на систему, т.е.


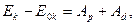
Где  - работа потенциальных сил,
- работа потенциальных сил, 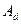 - работа непотенциальных сил ( например сил трения).
- работа непотенциальных сил ( например сил трения).
Учитывая, что работа потенциальных сил равна изменению потенциальной энергии 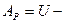
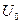 , получим закон изменения механической энергии:
, получим закон изменения механической энергии:
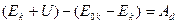 .
.
Изменение полной механической энергии системы равно работе всех непотенциальных сил.
12. Консервативная система – система, в которой отсутствуют непотенциальные силы, т.е. 
13. Замкнутая консервативная система – система, на которую не действуют внешние силы.
14. Закон сохранения механической энергии – полная механическая энергия замкнутой консервативной системы не изменяется с течением времени.
Этот вывод следует из закона изменения механической энергии, если принять 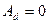 :
:
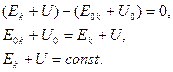
Применение закона сохранения энергии значительно упрощает решение задач кинематики. Пусть тело массы m находясь на поверхности Земли, получило начальную скорость 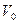 , направленную вертикально вверх. Для того, чтобы определить максимальную высоту, на которую поднимется тело, применим закон сохранения энергии. Полная механическая энергия тела у поверхности Земли согласно закону сохранения энергии равна его полной механической энергии на максимальной высоте. Учитывая, что потенциальная энергия тела у поверхности Земли равна нулю
, направленную вертикально вверх. Для того, чтобы определить максимальную высоту, на которую поднимется тело, применим закон сохранения энергии. Полная механическая энергия тела у поверхности Земли согласно закону сохранения энергии равна его полной механической энергии на максимальной высоте. Учитывая, что потенциальная энергия тела у поверхности Земли равна нулю 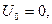 а кинетическая энергия на максимальной высоте равна нулю запишем
а кинетическая энергия на максимальной высоте равна нулю запишем
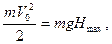
отсюда получим 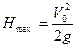 .
.
15.Центр тяжести –точка , к которой приложена сила тяжести тела. Центр тяжести совпадает с центром масс, поэтому под действием силы тяжести тело движется поступательно. Вычисляя перемещение тела при поступательном движении, мы вычисляем перемещение его центра тяжести.
Когда условия задачи позволяют рассматривать тело как материальную точку как материальную точку, то этой точкой является центр тяжести, в котором сосредоточена вся масса тела.
В выражении потенциальной энергии тела вблизи поверхности Земли 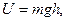 h – высота центра тяжести тела над поверхностью Земли. Например, центр тяжести однородного цилиндрического столба массы m и длиной l установленного вертикально находится в его середине, т.е. на высоте
h – высота центра тяжести тела над поверхностью Земли. Например, центр тяжести однородного цилиндрического столба массы m и длиной l установленного вертикально находится в его середине, т.е. на высоте  поэтому его потенциальная энергия равна
поэтому его потенциальная энергия равна
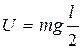 .
.
Дата добавления: 2015-08-08; просмотров: 5653;
