Лекция – 14. Механические волны.

1. Волна.

2. Механическая волна.

3. Источник механических волн.

4. Точечный источник волн.

5. Поперечная волна.

6. Продольная волна.

7. Фронт волны.

8. Луч.

9. Периодические волны.

10. Гармоническая волна.

11. Длина волны.

12. Скорость распространения.

13. Зависимость скорости волны от свойств среды.

14. Принцип Гюйгенса.

15. Отражение и преломление волн.

16. Закон отражения волн.

17. Закон преломления волн.

18. Уравнение плоской волны.

19. Энергия и интенсивность волны.

20. Принцип суперпозиции.

21. Когерентные колебания.

22. Когерентные волны.

23. Интерференция волн. а) условие интерференционного максимума, б) условие интерференционного минимума.

24. Интерференция и закон сохранения энергии.

25. Дифракция волн.

26. Принцип Гюйгенса – Френеля.

27. Поляризованная волна.

28. Звук.

29. Громкость звука.

30. Высота тона звука.

31. Тембр звука.

32. Ультразвук.

33. Инфразвук.

34. Эффект Доплера.

1.Волна –это процесс распространения колебаний какой-либо физической величины в пространстве. Например, звуковые волны в газах или в жидкостях представляют собой распространение колебаний давления и плотности в этих средах. Электромагнитная волна – это процесс распространения в пространстве колебаний напряженности электрического магнитного полей.

Энергию и импульс можно переносить в пространстве путём переноса вещества. Любое движущееся тело обладает кинетической энергией. Следовательно оно переносит кинетическую энергию, перенося вещество. Это же тело будучи нагретым, перемещаясь в пространстве переносит энергию тепловую, перенося вещество.

Частицы упругой среды связаны между собой. Возмущения, т.е. отклонения от положения равновесия одной частицы передаются соседним частицам, т.е. энергия и импульс передаются от одной частицы соседним частицам, при этом каждая частица остаётся около своего положения равновесия. Таким образом, энергия и импульс передаются по цепочке от одной частице к другой и переноса вещества при этом не происходит.

Итак, волновой процесс есть процесс переноса энергии и импульса в пространстве без переноса вещества.

2. Механическая волна или упругая волна – возмущение (колебание), распространяющееся в упругой среде. Упругой средой, в которой распространяются механические волны, является воздух, вода, дерево металлы и другие упругие вещества. Упругие волны называют звуковыми волнами.

3. Источник механических волн – тело, совершающее колебательное движение, находясь в упругой среде, например колеблющиеся камертоны , струны, голосовые связки.

4. Точечный источник волн –источник волны, размерами которого можно пренебречь по сравнению с расстоянием, на которое распространяется волна.

5. Поперечная волна –волна, в которой частицы среды колеблются в направлении перпендикулярном к направлению распространения волны. Например, волны на поверхности воды – поперечные волны, т.к. колебания частиц воды происходят в направлении перпендикулярном направлению к поверхности воды, а волна распространяется по поверхности воды. Поперечная волна распространяется вдоль шнура, один конец которого закреплён, другой совершает колебания в вертикальной плоскости.

Поперечная волна может распространяться лишь по границе раздела дух разных сред.

6. Продольная волна –волна, в которой колебания происходят в направлении распространения волны. Продольная волна возникает в длинной спиральной пружине, если один её конец подвергается периодическим возмущениям, направленным вдоль пружины. Упругая волна, бегущая вдоль пружины представляет собой распространяющиеся последовательности сжатия и растяжения (Рис. 88)

Продольная волна может распространяться только внутри упругой среды например, в воздухе, в воде. В твёрдых телах и в жидкостях могут распространяться одновременно как поперечные, так и продольные волны, т.к. твёрдое тело и жидкость всегда ограничены поверхностью – поверхностью раздела двух сред. Например, если стальной стержень ударить в торец молотком, то в нём начнёт распространяться упругая деформация. По поверхности стержня побежит поперечная волна, а внутри него будет распространяться волна продольная ( сжатия и разрежения среды) (Рис.89).

7. Фронт волны ( волновая поверхность)– геометрическое место точек, колеблющихся в одинаковых фазах. На волновой поверхности фазы колеблющихся точек в рассматриваемый момент времени имеют одно и тоже значение. Если в спокойное озеро бросить камень, то по поверхности озера от места его падения начнут распространяться поперечные волны в виде окружности, с центром в месте падения камня. В этом примере фронт волны представляет собой окружность.

В сферической волне фронт волны есть сфера. Такие волны порождаются точечными источниками.

На очень больших расстояниях от источника можно пренебречь кривизной фронта и считать фронт волны плоским. В этом случае волна называется плоской.

8. Луч – прямаялиниянормальная к волновой поверхности. В сферической волне лучи направлены вдоль радиусов сфер от центра, где расположен источник волн (Рис.90).

В плоской волне лучи направлены перпендикулярно к поверхности фронта (Рис. 91).

9. Периодические волны. Рассуждая о волнах мы подразумевали однократное возмущение, распространяющееся в пространстве.

Если же источник волн совершает непрерывные колебания, то в среде возникают бегущие одна за одной упругие волны. Такие волны называют периодическими.

10. Гармоническая волна – волна, порождаемая гармоническими колебаниями. Если источник волн совершает гармонические колебания, то он порождает гармонические волны – волны в которых частицы колеблются по гармоническому закону.

11. Длина волны.Пусть гармоническая волна распространяется вдоль оси OX, а колебания в ней происходят в направлении оси OY. Эта волна поперечная и её можно изобразить в виде синусоиды (Рис.92).

Такую волну можно получить, вызывая колебания в вертикальной плоскости свободного конца шнура.

Длиной волны 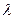называют расстояние между двумя ближайшими точками А и В, колеблющимися в одинаковых фазах (Рис. 92).

12. Скорость распространения волны – физическая величина численно равная скорости распространения колебаний в пространстве. Из Рис. 92 следует, что время за которое колебание распространяется от точки до точки А до точки В, т.е. на расстояние длины волны равно периоду колебаний. Поэтому скорость распространения волны равна

.

13. Зависимость скорости распространения волны от свойств среды. Частота колебаний при возникновении волны зависит только от свойств источника волны и не зависит от свойств среды. От свойств среды зависит скорость распространения волны. Поэтому длина волны изменяется при переходе границы раздела двух разных сред. Скорость волны зависит от связи между атомами и молекулами среды. Связь между атомами и молекулами в жидкостях и твёрдых телах значительно более жесткая, чем в газах. Поэтому скорости звуковых волн в жидкостях и твёрдых телах значительно больше, чем в газах. В воздухе скорость звука при нормальных условиях равна 340 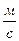, в воде 1500 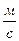, а в стали 6000 .

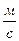Средняя скорость теплового движения молекул в газах с понижением температуры уменьшается и как следствие скорость распространения волны в газах уменьшается. В среде более плотной, а следовательно более инертной, скорость волны меньше. Если звук распространяется в воздухе то его скорость зависит от плотности воздуха. Там , где плотность воздуха больше, там скорость звука меньше. И наоборот там, где плотность воздуха меньше там скорость звука больше. Вследствие этого при распространении звука фронт волны искажается. Над болотом или над озером особенно в вечернее время плотность воздуха вблизи поверхности из- за водяных паров больше чем на некоторой высоте. Поэтому скорость звука вблизи поверхности воды меньше, чем на некоторой высоте. Вследствие этого фронт волны разворачивается таким образом, что верхняя часть фронта всё больше изгибается в направлении к поверхности озера. Получается так, что энергия волны идущей вдоль поверхности озера и энергия волны идущей под углом к поверхности озера складываются. Поэтому в вечернее время звук хорошо распространяется на озером. Даже тихий раговор можно услышать, стоя на противоположном берегу.

14. Принцип Гюйгенса – каждая точка поверхности, которой достигла в данный момент волна является источником вторичных волн. Проведя поверхность касательную к фронтам всех вторичных волн, получим фронт волны в следующий момент времени.

Рассмотрим для примера волну, распространяющуюся по поверхности воды из точки О (Рис.93) Пусть в момент времени t фронт имел форму окружности радиуса R с центром в точке О. В следующий момент времени 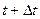каждая вторичная волна будет иметь фронт в форме окружности радиуса 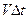, где V – скорость распространения волны. Проведя поверхность касательную к фронтам вторичных волн, получим фронт волны в момент времени 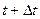(Рис. 93)

Если волна распространяется в сплошной среде, то фронт волны представляет собой сферу.

15. Отражение и преломление волн. При падении волны на поверхность раздела двух различных сред каждая точка этой поверхности согласно принципу Гюйгенса становится источником вторичных волн, распространяющихся по обе стороны от поверхности радела. Поэтому при переходе границы раздела двух сред волна частично отражается и частично проходит через эту поверхность. Т.к. среды различные, то и скорость волн в них различна. Поэтому при переходе границы раздела двух сред направление распространения волы изменяется, т.е. происходит преломление волны. Рассмотрим на основе принципа Гюйгенса процесс и законы отражения и преломления полн.

16. Закон отражения волн. Пусть на плоскую поверхность раздела двух различных сред падает плоская волна. Выделим в ней участок между двумя лучам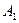и и 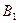(Рис.94)

Угол падения – угол 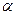- между лучом падающим и перпендикуляром к поверхности раздела в точке падения.

Угол отражения – угол 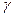между лучом отраженным и перпендикуляром к поверхности раздела в точке падения.

В момент когда, луч 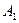достигнет поверхности раздела в точке 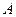, эта точка станет источником вторичных волн. Фронт волны в этот момент отмечен отрезком прямой АС (Рис.94). Следовательно, лучу 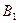еще предстоит в этот момент пройти до поверхности раздела путь СВ . Пусть луч 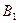проходит этот путь за время 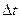. Падающий и отраженный лучи распространяются по одну сторону о поверхности раздела поэтому их скорости одинаковы и равны V. Тогда .

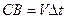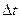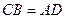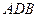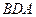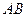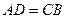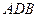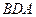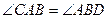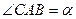За время вторичная волна из точки А пройдёт путь . Следовательно . Прямоугольные треугольники и равны, т.к. - общая гипотенуза и катеты . Из равенства треугольников и следует равенство углов . Но и 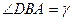, т.е. .

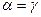Теперь сформулируем закон отражения волн: луч падающий , луч отраженный , перпендикуляр к границе раздела двух сред, восставленный в точке падения лежат в одной плоскости; угол падения равен углу отражения.

17. Закон преломления волн. Пусть через плоскую границу раздела двух сред проходит плоская волна. Причём угол падения отличен от нуля (Рис.95).

Угол преломления – угол 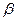между лучом преломлённым и перпендикуляром к границе раздела, восставленным в точке падения.

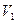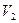Обозначим и скорости распространения волн в средах 1 и 2. В тот момент, когда луч 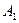достигнет границы раздела в точке А , эта точка станет источником волн, распространяющихся во второй среде – луч 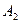, а лучу 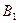ещё предстоит пройти путь 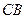до поверхности радела. Пусть 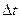- время, за которое луч 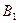проходит путь СВ, тогда 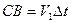. За это же время во второй среде луч 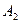пройдёт путь 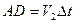. Т.к. 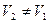, то и .

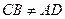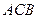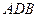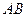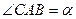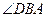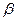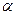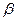Треугольники и прямоугольные с общей гипотенузой , и = , как углы с взаимно перпендикулярными сторонами. Для углов и запишем следующие равенства

.

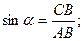
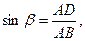
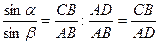Учитывая, что 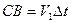, , 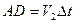получим

.

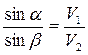Теперь сформулируем закон преломления волн: Луч падающий, луч преломлённый и перпендикуляр к границе раздела двух сред, восставленный в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух данных сред и называется относительным показателем преломления для двух данных сред.

18. Уравнение плоской волны.Частицы среды, находящиеся на расстоянии S от источника волн начинают колебаться только тогда, когда до неё дойдет волна. Если V есть скорость распространения волны, то колебания начнутся с опозданием на время

.

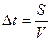Если источник волн колеблется по гармоническому закону 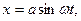то для частицы, находящейся на расстоянии S от источника, закон колебаний запишем в виде

.

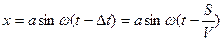Введём величину 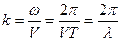, называемую волновым числом. Оно показывает, сколько длин волн укладывается на расстоянии равном 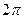единиц длины. Теперь закон колебаний частицы среды находящейся на расстоянии S от источника запишем в виде

.

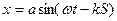Это уравнение определяет смещение колеблющейся точки, как функции времени и расстояния от источника волн и называется уравнением плоской волны.

19. Энергия и интенсивность волны. Каждая частица, до которой дошла волна колеблется и следовательно обладает энергией. Пусть в некотором объёме 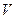упругой среды распространяется волна с амплитудой А и циклической частотой 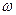. Это значит , что средняя энергия колебаний в этом объёме равна

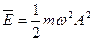, где m – масса выделенного объёма среды.

Средняя плотность энергии ( средняя по объёму) есть энергия волны в единице объёма среды

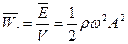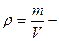, где плотность среды.

Интенсивность волны – физическая величина, численно равная энергии, которую переносит волна за единицу времени через единицу площади плоскости перпендикулярной к направлению распространения волны ( через единицу площади фронта волны), т.е.

.

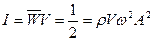Средняя мощность волны есть средняя полная энергия, переносимая волной за единицу времени через поверхность с площадью S . Среднюю мощность волны получим, умножив интенсивность волны на площадь S

.

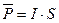20.Принцип суперпозиции (наложения). Если в упругой среде распространяются волны от двух и более источников, то как показывают наблюдения, волны проходят одна через другую совершенно не влияя друг на друга. Иными словами волны не взаимодействуют друг с другом. Это объясняется тем что в пределах в пределах упругой деформации сжатия и растяжения в одном направлении никоим образом не влияют на упругие свойства по другим направлениям.

Таким образом, каждая точка среды куда приходят две и более волны принимает участие в колебаниях, вызванных каждой волной. При этом результирующее смещение частицы среды в любой момент времени равно геометрической суммой смещений, вызываемых каждым из складывающихся колебательных процессов. В этом и состоит суть принципа суперпозиции или наложения колебаний.

Результат сложения колебаний зависит от амплитуды, частоты и разности фаз складывающихся колебательных процессов.

21. Когерентные колебания – колебания с одинаковой частотой и постоянной в времени разностью фаз.

22.Когерентные волны – волны одинаковой частоты или одинаковой длины волны, разность фаз которых в данной точке пространства остаётся постоянной во времени.

23.Интерференция волн – явление увеличения или уменьшения амплитуды результирующей волны при наложении двух и более когерентных волн.

а ) .Условия интерференционного максимума. Пусть волны от двух когерентных источников 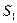и 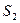встречаются в точке А (Рис.96).

Смещения частиц среды в точке А , вызванные каждой волной в отдельности запишем согласно уравнению волны в виде

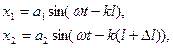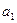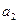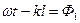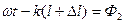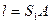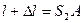где и , , - амплитуды и фазы колебаний, вызванных волнами в точке А, и - расстояния точки, 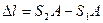- разность эти расстояний или разность хода волн.

Из-за разности хода волн вторая волна запаздывает по сравнению с первой. Это значит, что фаза колебаний в первой волне опережает фазу колебаний во второй волне, т.е. 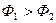. Их разность фаз остается постоянной во времени.

Для того, чтобы в точке А частицы совершали колебания с максимальной амплитудой , гребни обеих волн или их впадины должны достигнуть точки А одновременно в одинаковых фазах или с разностью фаз равной 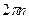, где n – целое число, а 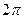- есть период функций синуса и косинуса,

,

,

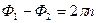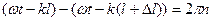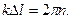Здесь 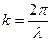, поэтому условие интерференционного максимума запишем в виде

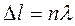, где - целое число .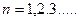

Итак, при наложении когерентных волн амплитуда результирующего колебания максимальна, если разность хода волн равна целому числу длин волн.

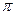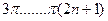б ) Условие интерференционного минимума. Амплитуда результирующего колебания в точке А минимальна, если в эту точку одновременно придут гребень и впадина двух когерентных волн. Это значит, сто волны придут в эту точку в противофазе, т.е. разность их фаз равна или , где 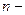целое число.

Условие интерференционного минимума получим, проведя алгебраические преобразования:

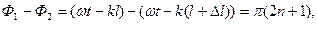
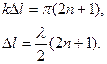
Таким образом, амплитуда колебаний при наложении двух когерентных волн минимальна, если разность хода волн равна нечетному числу полуволн.

24. Интерференция и закон сохранения энергии.При интерференции волн в местах интерференционных минимумов энергия результирующих колебаний меньше, чем энергия интерферирующих волн. Но в местах интерференционных максимумов энергия результирующих колебаний превышает сумму энергий интерферирующих волн настолько, насколько уменьшилась энергия в местах интерференционных минимумов.

При интерференции волн энергия колебаний перераспределяется в пространстве, но закон сохранения строго выполняется.

25.Дифракция волн – явление огибания волной препядствия, т.е. отклонение от прямолинейного распространения волн.

Дифракция особенно хорошо заметна в случае, когда размеры препядствия меньше длины волны или сравнимы с ней. Пусть на пути распространения плоской волны расположен экран с отверстием, диаметр которого сравним с длиной волны (Рис. 97).

По принципу Гюйгенса каждая точка отверстия становится источником таких же волн . Размер отверстия настолько мал, что все источники вторичных волн расположены так близко друг к другу, что их все можно считать одной точкой – одним источником вторичных волн.

Если на пути волны поставить препядствие, размер которого сравним с длиной волны, то края по принципу Гюйгенса становятся источником вторичных волн. Но размеры препядствия настолько малы, что края его можно считать совпадающими, т.е. само препядствие является точечным источником вторичных волн ( Рис.97).

Явление дифракции легко наблюдается при распространении волн по поверхности воды. Когда волна достигает тонкой, неподвижной палочки, она становится источником волн (Рис. 99).

25. Принцип Гюйгенса-Френеля. Если же размеры отвепстия значительно превышают длину волны, то волна, проходя отверстие распространяется прямолинейно (Рис.100).

Если размеры препядствия значительно превышают длину волны, то за препядствием образуется зона тени (Рис.101). Эти опыты противоречат принципу Гюйгенса. Французский физик Френель дополнил принцип Гюйгенса представлением о когерентости вторичных волн. Каждая точка, в которую пришла волна становится источником таких же волн, т.е. вторичных когерентных волн. Поэтому волны отсутствуют только в тех местах, в которых для вторичных волн выполняются условия интерференционного минимума.

26. Поляризованная волна – поперечная волна, в которой колебания всех частиц происходят в одной плоскости. Если свободный конец шнура совершает колебания в одной плоскости, то по шнуру распространяется плоскополяризованная волна. Если свободный конец шнура совершает колебания в различных направлениях, то волна распрстраняющаяся по шнуру не пеоляризована. Если на пути неполяризованной волны поставить препядствие в виде узкой щели, то после прохождении щели волна становится поляризованной, т.к. щель пропускает колебания шнура, происходящие вдоль неё.

Если на пути поляризованной волны поставить вторую щель параллельную первой, то волна свободно пройдет через неё (Рис.102).

Если же вторую щель расположить под прямым углом по отношению к первой, то распространение волы прекратится. Устройство, которое выделяет колебания, происходящие в одной определённой плоскости называется поляризатором (первая щель). Устройство, которое определяет плоскость поляризации называется анализатором.

27.Звук –это процесс распространения сжатий и разрежений в упругой среде например, в газе, жидкости или в металлах. Распространение сжатий и разрежений происходит в результате столкновения молекул.

28. Громкость звука это сила воздействия звуковой волны на барабанную перепонку человеческого уха, которая от звукового давления.

Звуковое давление – это дополнительное давление, возникающее в газе или жидкости при распространении звуковой волны. Звуковое давление зависит от амплитуды колебании источника звука. Если заставить звучать камертон лёгким ударом , то мы получим одну громкость. Но, если камертон ударить сильнее, то амплитуда его колебаний увеличится и он зазвучит громче. Таким образом громкость звука определяется амплитудой колебании источника звука, т.е. амплитудой колебаний звукового давления.

29. Высота тона звукаопределяется частотой колебаний. Чем больше частота звука, тем выше тон.

Звуковые колебания происходящие по гармоническому закону воспринимаются как музыкальный тон. Обычно звук это сложный звук, который представляет собой совокупность колебаний с близкими частотами.

Основной тон сложного звука – это тон соответствующий наименьшей частоте в наборе частот данного звука. Тоны соответствующие остальным частотам сложного звука называются обертонами.

30. Тембр звука. Звуки одним и тем же основным тоном различаются тембром, который определяется набором обертонов.

У каждого человека свой только ему присущий тембр. Поэтому мы всегда можем отличить голос одного человека от голоса другого человека, даже в том случае, когда их основные тоны одинаковы.

31.Ультразвук. Человеческое ухо воспринимает звуки , частоты которых заключены в пределах от 20Гц до 20000Гц.

Звуки с частотами более 20000Гц называются ультразвуками. Ультразвуки распространяются в виде узких пучков и используются в гидролокации и дефектоскопии. С помощью ультразвука можно определить глубину морского дна и обнаружить дефекты в различных деталях.

Например, если рельс не имеет трещин, то ультразвук испущенный из одного конца рельса, отразившись от другого его конца даст только одно эхо. Если же есть трещины, то ультразвук будет отражаться от трещин и приборы будут фиксировать несколько эхо. С помощью ультразвука обнаруживают подводные лодки, косяки рыб. Летучая мышь ориентируется в пространстве с помощью ультразвука.

32. Инфразвук– звук с частотой ниже 20Гц. Эти звуки воспринимаются некоторыми животными . Их источником часто бывают колебания земной коры при землетрясениях.

33. Эффект Доплера – это зависимость частоты воспринимаемой волны от движения источника или приёмника волн.

Пусть на поверхности озера покоится лодка и волны бьются о её борт с некоторой частотой 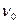. Если лодка начнёт движение против направления распространения волн, то частота ударов волн о борт лодки станет больше. Причём, чем больше скорость лодки, тем больше частота ударов волн о борт. И наоборот при движении лодки в направлении распространения волн частота ударов станет меньше. Эти рассуждения легко понять из Рис. 103.

Чем больше скорость встречного движения, тем меньшее время затрачивается на прохождение расстояния между двумя ближайшими гребнями, т.е. тем меньше период волны и тем больше частота волны относительно лодки.

Если же наблюдатель неподвижен, но движется источник волн, то частота волны воспринимаемая наблюдателем зависит от движения источника.

Пусть по неглубокому озеру по направлению к наблюдателю идет цапля. Каждый раз, когда она опускает ногу в воду от этого места кругами расходятся волны. И каждый раз расстояние между первой и последней волнами уменьшается, т.е. на меньшем расстоянии укладывается большее число гребней и впадин. Поэтому для неподвижного наблюдателя по направлению к которому идет цапля частота увеличивается. И наоборот для неподвижного наблюдателя, находящегося в диаметрально противоположной точке на большем расстоянии столько же гребней и впадин. Поэтому для этого наблюдателя частота уменьшается (Рис.104).