Лекция – 10. Статика.
1. Статика твёрдого тела.
2. Абсолютно твёрдое тело.
3. Первое условие равновесия абсолютно твёрдого тела.
4. Правило моментов – второе условие равновесия абсолютно твёрдого тела.
5. Правило равновесия рычага (правило рычага)
6. Коэффициент полезного действия (КПД) механизмов.
1. Статика твёрдого тела – часть механики, изучающая условия равновесия твёрдого тела. Действие сил на тело вызывает его деформацию. Поэтому, изучая условия равновесия тела, мы имеем дело с деформированным телом, т.е. с другим телом. По этой причине задачи на расчёт условий равновесия тел с учётом их деформации весьма сложны. Мы будем решать задачи, в которых деформации тела столь незначительны, что ими можно пренебречь и считать тело абсолютно твёрдым.
2. Абсолютно твёрдое тело – система материальных точек, расстояния между которыми остаются неизменными.
3. Первое условие равновесия абсолютно твёрдого тела. Если тело находится в состоянии покоя, то говорят, что тело находится в равновесии. В этом случае ускорение каждого его элемента равно нулю и согласно второму закону Ньютона геометрическая сумма всех сил, действующих на любой элемент тела равна нулю:
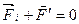 ,
,
Где i – номер элемента, 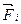 - сумма всех внешних сил, действующих на i - й элемент,
- сумма всех внешних сил, действующих на i - й элемент, 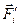 - сумма всех внутренних сил, действующих на i – й элемент.
- сумма всех внутренних сил, действующих на i – й элемент.
Складывая все силы, действующие на все элементы тела, получим
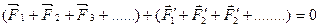 .
.
Векторная сумма всех внутренних сил равна нулю, т.к. согласно третьему закону Ньютона, силы с которыми попарно взаимодействуют элементы тела равны по модулю и противоположны по направлению
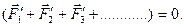
Таким образом, для равновесия абсолютно твёрдого тела получим условие для внешних сил – первое условие равновесия
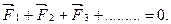
Итак, твёрдое тело находится в равновесии, если геометрическая сумма все внешних сил, приложенных к нему равна нулю.
Т.к. геометрическая сумма всех внешних сил равна нулю, то равна нулю и сумма проекций всех этих сил на любую ось:
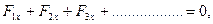
что также является первым условием равновесия абсолютно твёрдого тела.
Итак, первым условием равновесия абсолютно твёрдого тела является равенство нулю геометрической суммы всех внешних сил либо равенство нулю суммы проекций этих сил на любую ось.
4.Момент силы. Правило моментов - второе условие равновесия абсолютно твёрдого тела. Пусть в точках А и В свободного тела приложены две силы, равные по модулю противоположные по направлению (пара сил) 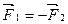 , т.е.
, т.е. 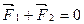 (Рис.59)
(Рис.59)
 Очевидно, что эти силы заставят тело поворачиваться. Поэтому равенство нулю геометрической суммы всех внешних сил, приложенных к телу есть условие необходимое, но недостаточное для его равновесия.
Очевидно, что эти силы заставят тело поворачиваться. Поэтому равенство нулю геометрической суммы всех внешних сил, приложенных к телу есть условие необходимое, но недостаточное для его равновесия.
Это объясняется тем, что хотя сумма всех внешних сил, приложенных к телу равна нулю, сумма всех внешних сил, приложенных к каждому элементу тела, может быть не равна нулю.
Рассмотрим рычаг (Рис. 60). Пусть в точках А и В рычага приложены силы 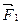 и
и 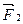 соответственно. В точке О приложена сила реакции оси рычага
соответственно. В точке О приложена сила реакции оси рычага 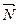 , направленная вертикально вверх.
, направленная вертикально вверх.
 При повороте рычага на очень малый угол
При повороте рычага на очень малый угол 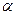 точки А и В проходят пути
точки А и В проходят пути 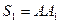 и
и 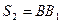 , т.е. при малых углах поворота можно пренебречь кривизной пути считать длину дуги раной длине хорды.
, т.е. при малых углах поворота можно пренебречь кривизной пути считать длину дуги раной длине хорды.
Работу сил 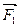 и
и 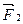 запишем в виде
запишем в виде
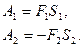
Работа силы 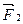 отрицательна, т.к. она направлена против перемещения точки В .Точка О неподвижна поэтому сила
отрицательна, т.к. она направлена против перемещения точки В .Точка О неподвижна поэтому сила 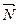 работу не совершает. Выражая угол
работу не совершает. Выражая угол 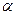 в радианах получим
в радианах получим
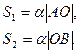
Теперь работу сил 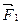 и
и 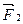 запишем в виде
запишем в виде
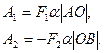
При малых углах поворота радиусы вращения точек А и В можно считать перпендикулярными направлениям действия сил 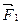 и
и 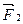 .
.
Плечо силы – длина перпендикуляра, опущенного из оси вращения на линию действия силы. Обозначим плечо силы буквой d , тогда 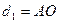 - плечо силы
- плечо силы 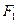 , а
, а 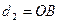 - плечо силы
- плечо силы 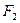 . Теперь работу этих сил запишем в виде
. Теперь работу этих сил запишем в виде

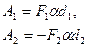
Величины 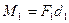 и
и 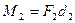 называют моментами сил
называют моментами сил 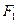 и
и 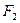 относительно оси вращения.
относительно оси вращения.
Моментом силы относительно оси вращения называют произведение модуля силы на еёплечо.
Момент силы, направленной против часовой стрелки относительно оси вращения считают положительным. Момент силы, направленной по часовой стрелке относительно оси вращения считают отрицательным. Пользуясь определением момента силы, работу сил 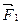 и
и 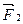 запишем в виде
запишем в виде
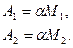
Полная работа внешних сил 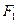 и
и 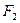 равна сумме их работ:
равна сумме их работ:
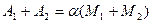 .
.
Когда тело находится в положении равновесия – в состоянии покоя, полная работа всех внешних сил равна нулю. Следовательно, в положении равновесия
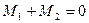 ,
,
Что и является вторым условием необходимым для равновесия тела. Это условие называется правилом моментов.
Итак, сформулируем правило моментов: при равновесии тела сумма моментов всех внешних сил, действующих на него, относительно любой оси равна нулю. Это правило часто формулируется следующим образом:
При равновесии тела сумма моментов внешних сил, действующих на него по часовой стрелке, относительно любой оси равна сумме моментов внешних сил, действующих на него против часовой стрелки относительно той же оси.
Для произвольного числа внешних сил, необходимые и достаточные условия равновесия тела запишем в виде
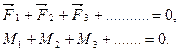
5. Правило равновесия рычага. Второе условие равновесия для рычага можно сформулировать следующим образом. При равновесии рычага моменты сил, действующих на него по часовой стрелке и против часовой стрелки относительно оси вращения равны по модулю, т.е.
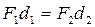 .
.
Из этого равенства получим правило рычага в виде равенства
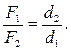
Рычаг находится в равновесии, если модули сил, действующих на него, обратно пропорциональны плечам этих сил.
Правило рычага было установлено экспериментально Архимедом около 287 – 212 г.г. до н. э.
Рычаг даёт выигрыш в силе, т.е. меньшей силой можно уравновесить силу значительно большую. Однако выигрыша в в работе рычаг не даёт ( 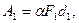
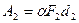 , но
, но 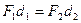 , поэтому
, поэтому 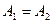 ).
).
Если же учесть трение на оси рычага, то при использовании рычага затраченная работа окажется больше работы полезной – работы которую нужно совершить. Рычаг, как любой механизм, облегчающий работу имеет коэффициент полезного действия (КПД).
6. Коэффициент полезного действия (КПД) механизмов. Между частями любого механизма существует трение. Поэтому , используя механизмы для облегчения труда, мы в действительности совершаем работу 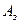 ( затраченная работа) больше той, которую необходимо выполнить -
( затраченная работа) больше той, которую необходимо выполнить - 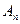 (полезная работа).
(полезная работа).
Коэффициентом полезного действия механизма называют отношение работы полезной к работе затраченной, выраженное в процентах:
КПД = 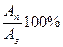 .
.
В качестве примера вычислим КПД наклонной плоскости (Рис. 61). Пусть тело массы m необходимо поднять на высоту h. Если это делать непосредственно, то будет совершена работа 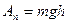 , при этом мы будем прилгать силу
, при этом мы будем прилгать силу 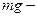 силу тяжести.
силу тяжести.
 Если же этот предмет втаскивать по наклонной плоскости с углом наклона
Если же этот предмет втаскивать по наклонной плоскости с углом наклона 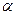 и длиной l то мы будем прилагать силу
и длиной l то мы будем прилагать силу 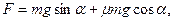 где
где 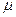 - коэффициент трения. Сила
- коэффициент трения. Сила 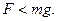 затраченная работа при это равна
затраченная работа при это равна 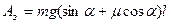 .
.
Для сокращения записи обозначим КПД греческой буквой 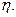 Теперь КПД наклонной плоскости запишем в виде
Теперь КПД наклонной плоскости запишем в виде
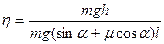 .
.
Учитывая далее, что 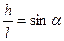 и сокращая на
и сокращая на 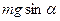 , получим коэффициент полезного действия наклонной плоскости
, получим коэффициент полезного действия наклонной плоскости
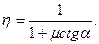
Дата добавления: 2015-08-08; просмотров: 2052;
