Лекция – 11. Гидроаэростатика.
1. Текучие среды (флюиды).
2. Механика текучих сред.
3. Гидроаэростатика.
4. Гидроаэродинамика.
5. Давление.
6. Закон Паскаля.
7. Гидростатическое давление.
8. Закон сообщающихся сосудов.
9. Гидравлический пресс.
10. Закон Архимеда.
11. Центр давления.
12. Условия плавания тел.
13. Атмосферное давление.
14. Нормальное атмосферное давление.
15. Изменение атмосферного давления с высотой.
16. Соотношение между паскалем и мм. рт. ст.
1. Текучие среды (флюиды) – жидкости и газы. Их отличительной особенностью является текучесть, обусловленная малыми силами трения при относительном движении соседних слоёв. 2.Механика текучих сред или гидроаэромеханика – раздел физики, изучающий законы движения и равновесия текучих сред, а также их взаимодействие с твёрдыми телами. 3 .Гидроаэростатика – раздел механики текучих сред, изучающий условия и закономерности равновесия текучих сред под воздействием приложенных к ним сил и условия равновесия твёрдых тел, расположенных в них.
4. Гидроаэродинамика –раздел механики текучих сред, изучающий законы движения текучих сред, а также взаимодействие текучих сред с твёрдыми телами при их относительном движении.
В механике текучих сред не учитывается молекулярное строение жидкостей и газов, т.е. жидкости и газы рассматриваются как сплошные среды.
В отличие от твёрдых тел флюиды не сохраняют своей формы, а принимают форму того сосуда, в который они заключены. Жидкости отличаются от газов наличием свободной поверхности (поверхностного слоя), газы занимают весь объём сосуда. Кроме того, при одинаковых условиях плотность жидкости больше плотности газа.
 5. Давление – физическая величина, равная отношению силы, действующей нормально к поверхности к площади этой поверхности. Нормально – значит перпендикулярно к касательной плоскости в точке касания (Рис. 62)
5. Давление – физическая величина, равная отношению силы, действующей нормально к поверхности к площади этой поверхности. Нормально – значит перпендикулярно к касательной плоскости в точке касания (Рис. 62)
Выделим на данной поверхности около точки касания О участок с площадью 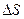 настолько малый, что его можно считать частью касательной плоскости. И пусть на этот участок действует нормально сила
настолько малый, что его можно считать частью касательной плоскости. И пусть на этот участок действует нормально сила 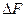 . Тогда по определению среднее давление действующее на этот участок равно
. Тогда по определению среднее давление действующее на этот участок равно
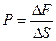 .
.
Уменьшая этот участок в пределе при 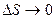 получим давление в данной точке О
получим давление в данной точке О
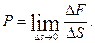

Если сила, действующая нормально к поверхности тела не зависит от точки приложения и равномерно распределена по его поверхности, то давление выражается формулой
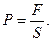
Силу давления запишем в виде 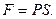
В СИ давление измеряется в паскалях (Па). Один паскаль – давление, которое оказывает сила в 1н, равномерно распределённая по площади один квадратный метр, т.е. 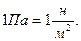
 6. Закон Паскаля (основной закон гидростатики).В состоянии покоя все частицы жидкости находятся в покое друг относительно друга. Следовательно, равнодействующая всех сил, действующих на данную частицу со стороны соседних частиц равна нулю.
6. Закон Паскаля (основной закон гидростатики).В состоянии покоя все частицы жидкости находятся в покое друг относительно друга. Следовательно, равнодействующая всех сил, действующих на данную частицу со стороны соседних частиц равна нулю.
Выделим внутри жидкости малый объём в форме прямой треугольной призмы (Рис.63).
Сечение призмы возьмём настолько малым, что давлением на торцевые грани можно пренебречь. Равнодействующая сил, действующих на боковые грани равна нулю, т.е.
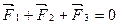 .
.
 Следовательно, эти силы составляют замкнутый треугольник подобный треугольнику в основании призмы. Углы этих треугольников равны, как углы с взаимно перпендикулярными сторонами (Рис.64). Эти треугольники подобны.
Следовательно, эти силы составляют замкнутый треугольник подобный треугольнику в основании призмы. Углы этих треугольников равны, как углы с взаимно перпендикулярными сторонами (Рис.64). Эти треугольники подобны.  Поэтому можем записать:
Поэтому можем записать:
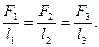
Умножив знаменатели на высоту d призмы, получим
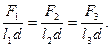
Учитывая, что в последнем равенстве знаменатели равны площадям соответствующих граней призмы, получим

Итак, давления производимые жидкостью на боковые грани призмы равны.
Уменьшая размеры призмы, в пределе получим, что в состоянии равновесия давления жидкости
в данной точке одинаковы по всем направлениям.
Если на жидкость оказывается давление извне, то это давление передаётся по всем направлениям без изменения.
Сформулируем теперь закон Паскаля: давление, производимое на жидкость или газ, передаётся во все точки по всем направлениям без изменения.
 7. Гидростатическое давление. Гидростатическая формула. Если жидкость или газ находится в поле тяжести, то давление, производимое верхними слоями, передается по всем направлениям одинаково. Величина этого давления зависит от глубины под поверхностью жидкости.
7. Гидростатическое давление. Гидростатическая формула. Если жидкость или газ находится в поле тяжести, то давление, производимое верхними слоями, передается по всем направлениям одинаково. Величина этого давления зависит от глубины под поверхностью жидкости.
Гидростатическое давление – давление, вызванное силой тяжести жидкости, зависит от глубины под поверхностью жидкости.
Выделим в жидкости объём 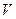 в форме цилиндра с площадью основания S, расположенного вертикально. На Рис. 65
в форме цилиндра с площадью основания S, расположенного вертикально. На Рис. 65 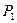 и
и 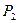 давление жидкости на верхнем и нижнем основаниях, т.е. на глубинах
давление жидкости на верхнем и нижнем основаниях, т.е. на глубинах 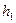 и
и 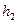 . Силы, действующие со стороны соседних частиц жидкости на боковую поверхность, уравновешены. На верхнее основание вертикально вниз действует сила
. Силы, действующие со стороны соседних частиц жидкости на боковую поверхность, уравновешены. На верхнее основание вертикально вниз действует сила 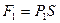 , на нижнее основание вертикально вверх действует сила
, на нижнее основание вертикально вверх действует сила 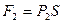 .
.
В состоянии равновесия сила тяжести цилиндра 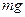 уравновешена разностью сил
уравновешена разностью сил 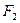 и
и 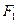 , т.е.
, т.е.
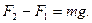
Учитывая, что 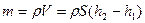 , где
, где 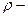 плотность жидкости запишем
плотность жидкости запишем
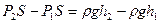 .
.
Сокращая на S , получим 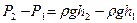 .
.
Давление жидкости у поверхности  равно атмосферному давлению, т.е.
равно атмосферному давлению, т.е.  . Поэтому давление жидкости на произвольной глубине h выражается гидростатической формулой:
. Поэтому давление жидкости на произвольной глубине h выражается гидростатической формулой:
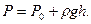
Давление, производимое столбом жидкости высотой h равно
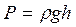 .
.
 8. Закон сообщающихся сосудов. Пусть в сообщающиеся сосуды налиты две разнородные жидкости, плотности которых
8. Закон сообщающихся сосудов. Пусть в сообщающиеся сосуды налиты две разнородные жидкости, плотности которых 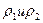 . Жидкости разделены подвижным поршнем В (Рис.66). Сосуды открыты, поэтому давления у поверхностных слоёв одинаковы и равны атмосферному давлению
. Жидкости разделены подвижным поршнем В (Рис.66). Сосуды открыты, поэтому давления у поверхностных слоёв одинаковы и равны атмосферному давлению 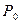 . Поршень В находится в покое, если выполняется условие:
. Поршень В находится в покое, если выполняется условие:
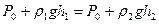 ,
,
 или
или 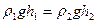 . Сокращая на g, получим закон сообщающихся сосудов. Высоты столбов разнородных жидкостей в сообщающихся сосудах обратно пропорциональны плотностям этих жидкостей, т.е.
. Сокращая на g, получим закон сообщающихся сосудов. Высоты столбов разнородных жидкостей в сообщающихся сосудах обратно пропорциональны плотностям этих жидкостей, т.е.
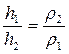 .
.
Если в сообщающихся сосудах находится однородная жидкость 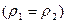 , то свободная поверхность жидкости во всех сосудах устанавливается на одном и том же уровне, независимо от формы сосуда (Рис.67).
, то свободная поверхность жидкости во всех сосудах устанавливается на одном и том же уровне, независимо от формы сосуда (Рис.67).
9.Гидравлический пресс представляет собой два сообщающихся цилиндра разного сечения с подвижными поршнями, заполненных маслом. Положим 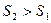 ,
, 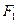 и
и 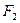 - силы, действующие на поршни
- силы, действующие на поршни 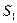 и
и 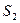 (Рис.68).
(Рис.68).
По закону Паскаля давление Р в обоих цилиндрах одинаково поэтому можно записать равенство

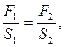
Из которого следует
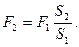
Таким образом, действуя на поршень меньшего сечения 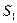 силой
силой 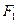 , на поршне большего сечения
, на поршне большего сечения 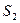 получим силу
получим силу 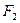 , превышающую силу
, превышающую силу 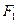 в
в 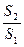 раз.
раз.
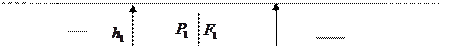 10. Закон Архимеда. Для упрощения рассуждений поместим в жидкость, плотность которой
10. Закон Архимеда. Для упрощения рассуждений поместим в жидкость, плотность которой 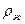 , тело цилиндрической формы. Цилиндр расположим вертикально (Рис.69),
, тело цилиндрической формы. Цилиндр расположим вертикально (Рис.69), 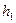 и
и 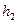 - глубины верхнего и нижнего оснований цилиндра под поверхностью жидкости, S – площадь основания цилиндра.
- глубины верхнего и нижнего оснований цилиндра под поверхностью жидкости, S – площадь основания цилиндра.
Равнодействующая сил, действующих со стороны жидкости на боковую поверхность цилиндра равна нулю.
На верхнее основание вертикально вниз действует сила 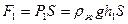 . На нижнее основание вертикально вверх действует сила
. На нижнее основание вертикально вверх действует сила 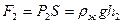 ,
, 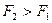 , т.к.
, т.к. 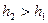 .
.
Равнодействующая сил 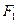 и
и 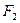 направлена вертикально вверх, называется силой Архимеда и равна
направлена вертикально вверх, называется силой Архимеда и равна
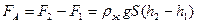 .
.
Учитывая, что 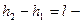 высота цилиндра,
высота цилиндра, 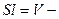 объём цилиндра получим выражение силы Архимеда в виде
объём цилиндра получим выражение силы Архимеда в виде
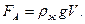
Здесь 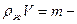 масса жидкости в объёме цилиндра, а
масса жидкости в объёме цилиндра, а 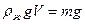 есть сила тяжести жидкости. Следовательно, сила Архимеда равна весу жидкости в объёме погруженного в неё тела. Теперь сформулируем закон Архимеда: “ На тело, погруженное в жидкость, действует выталкивающая сила, равная по модулю силе тяжести жидкости, вытесненной телом”.
есть сила тяжести жидкости. Следовательно, сила Архимеда равна весу жидкости в объёме погруженного в неё тела. Теперь сформулируем закон Архимеда: “ На тело, погруженное в жидкость, действует выталкивающая сила, равная по модулю силе тяжести жидкости, вытесненной телом”.
Закон Архимеда справедлив и для газов. Тело полностью погружено в газ а в жидкости тело может быть погружено не полностью так, что часть его остается над свободной поверхностью жидкости
Если тело погружено в жидкость не целиком и часть его объёма остаётся над свободной поверхностью жидкости, то сила Архимеда равна
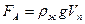 ,
,
Где 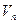 - объём части тела, погруженной под свободной поверхностью жидкости.
- объём части тела, погруженной под свободной поверхностью жидкости.
11.Центр давления – точка, к которой приложена сила Архимеда.
12. Условие плавания тел. Если при полном погружении тела, сила Архимеда по модулю больше силы тяжести тела, т.е. 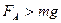 , то тело всплывает. Пусть плотность тела
, то тело всплывает. Пусть плотность тела 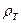 , тогда
, тогда 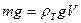 и из неравенства
и из неравенства 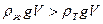 получим условие плавания тел
получим условие плавания тел
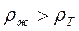 .
.
Если плотность тела больше плотности жидкости, т.е. 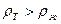 , то тело тонет.
, то тело тонет.
Если плотности тела и жидкости равны 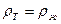 , то тело находится в равновесии на любой глубине.
, то тело находится в равновесии на любой глубине.
Для морских и речных судов, изготовленных из металла, средняя их плотность значительно меньше плотности воды. Поэтому современные суда обладают большой грузоподъемностью.
 13.Атмосферное давление. Наличие атмосферного давления было доказано экспериментально в 17 в. учеником Галилея Эванджелистой Торичелли.
13.Атмосферное давление. Наличие атмосферного давления было доказано экспериментально в 17 в. учеником Галилея Эванджелистой Торичелли.
Стеклянную трубку, запаянную с одного конца и заполненную ртутью, Торричелли, закрыв другой конец, перевернул и опустил в чашку со ртутью. Установив трубку вертикально он открыл её. Часть ртути вылилась в чашку, а другая её часть осталась в трубке. Высота столба, оставшейся в трубке ртути составила около 760 мм. Над ртутью в трубке образовалось безвоздушное пространство, которое принято называть Торичеллевой пустотой.
Ртуть из трубки не могла вылиться полностью потому, что на открытую поверхность ртути в чашке действует давление атмосферы (Рис.70).
Измеряя высоту столба ртути в трубке, можно получить представление об атмосферном давлении, выражаемом в миллиметрах ртутного столба. Если давление атмосферы повышается, то высота столба ртути увеличивается и наоборот с понижением атмосферного давления высота столба ртути уменьшается.
14.Нормальное атмосферное давление 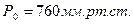 Это давление атмосферы на уровне моря при температуре ноль градусов по шкале Цельсия.
Это давление атмосферы на уровне моря при температуре ноль градусов по шкале Цельсия.
15. Изменение атмосферного давления с высотой.Вследствие большой сжимаемости газа его плотность существенно меняется с высотой, а именно уменьшается при увеличении высоты. Следовательно, с увеличением высоты уменьшается атмосферное давление. Эта зависимость выражается барометрической формулой 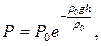 где
где 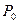 и
и 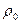 - давление и плотность воздуха на высоте h=0, т.е. на поверхности Земли.
- давление и плотность воздуха на высоте h=0, т.е. на поверхности Земли.
16. Соотношение между единицами измерения давления паскалем и миллиметром ртутного столба.
Давление, которое оказывает один миллиметр ртутного столба, вычислим по формуле 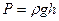 , где
, где 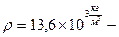 плотность ртути,
плотность ртути, 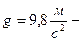 ускорение свободного падения,
ускорение свободного падения, 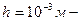 высота столба ртути
высота столба ртути

Итак , 1 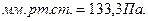
Дата добавления: 2015-08-08; просмотров: 1598;
