Задача № 9. Определить координаты центра тяжести плоского сечения, ограниченного осью х, квадратной параболой x = hy2/b2 и прямой линией х = h (рис

Определить координаты центра тяжести плоского сечения, ограниченного осью х, квадратной параболой x = hy²/b² и прямой линией х = h (рис. 1).

Определить координаты центра тяжести плоского сечения, ограниченного осью х, кубической параболой x = hy³/b³ и прямой линией x = h (рис. 2).

Определить координаты центра тяжести плоского сечения, ограниченного осью у, кубической параболой x = hy³/b³ и прямой линией у = в (рис. 2).

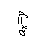
Решение к рис.1. Для нахождения центра тяжести воспользуемся формулами 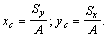В первую очередь по формуле 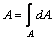определяем площадь поперечного сечения

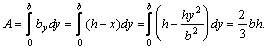
Затем по формулам находим статические моменты сечения:

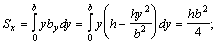
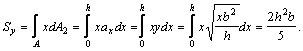
И, окончательно, по формулам 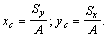определяем

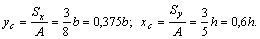
Ответ к рис 1: x_1c = 0,375b; y_1c = 0,6h.

Ответ к рис 2: x_1c = 4h/7; y_1c = 0,4b.

Ответ к рис.3: x_2c= 2h/7; y_2c= 0,8b.