Решение. Под действием внешней нагрузки в точках опор системы , и возникают реакции , , , ,
Под действием внешней нагрузки в точках опор системы 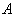 ,
, 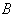 и
и 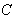 возникают реакции
возникают реакции 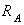 ,
, 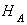 ,
, 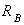 ,
, 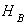 ,
, 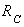 ,
, 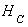 . Кроме того, в тягах возникают усилия соответственно
. Кроме того, в тягах возникают усилия соответственно 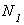 и
и 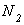 .
.
Для решения данной задачи необходимо по очереди рассмотреть равновесие двух абсолютно жестких стержней. Сначала рассекаем систему сечением 1-1 по тяге № 1 и рассматриваем равновесие нижнего бруса (рис. 2.30, б), а затем - равновесие верхнего бруса (рис. 2.30, а). Из условий равновесия для нижней части будем находить усилие в первой тяге 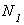 , а из условия равновесия для верхней -
, а из условия равновесия для верхней - 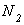 (при этом усилие
(при этом усилие 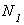 считается уже известным).
считается уже известным).
Для определения усилия 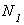 необходимо записать уравнение моментов относительно точки
необходимо записать уравнение моментов относительно точки 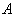 (рис. 2.30, б):
(рис. 2.30, б):
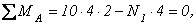
отсюда 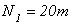 - усилие растяжения.
- усилие растяжения.
Теперь, считая усилие 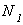 известным, необходимо рассмотреть равновесие средней части, для чего записать уравнение моментов относительно точки
известным, необходимо рассмотреть равновесие средней части, для чего записать уравнение моментов относительно точки 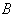 (рис. 2.30, а):
(рис. 2.30, а):

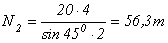 .
.
отсюда 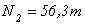 - усилие растяжения.
- усилие растяжения.
а) 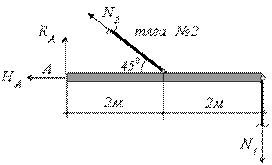
б) 
Рис.2.30
Далее, для каждой тяги записываем условие прочности и выражаем площади поперечных сечений 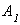 - площадь тяги № 1,
- площадь тяги № 1, 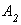 - площадь тяги № 2.
- площадь тяги № 2.
ТЯГА № 1:
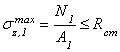 ,
,
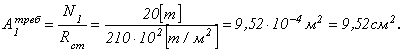
По сортаменту принимаем швеллер [ №10, 
Фактическая площадь сечения должна быть не меньше требуемой!
ТЯГА № 2:

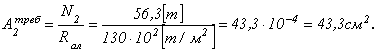
Алюминиевая тяга имеет круглое сечение, тогда требуемый диаметр:

Фактическая площадь круглого сечения:
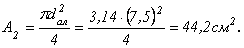
Дата добавления: 2015-08-08; просмотров: 654;
