Пример 16.
Два стальных (Е = 2·105 МПа) стержня, шарнирно соединенные в точке А, находятся под действием силы Р (рис. 2.33). Первый стержень имеет длинус и площадь поперечного сечения F, второй длину а и площадь - 2F.
1) Найти величины нормальных напряжений, действующих в стержнях.
2) Найти абсолютную и относительную деформации стержней.
Дано: Р = 130 кН, с = 1,5 м, а = 2 м, F = 12 см.

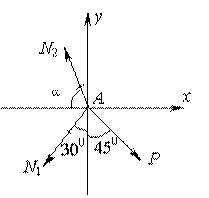
Рис.2.33Рис.2.34
Решение.
Стержни прикреплены к стене и соединены между собой шарнирами (точках В, С и А). Шарниры предполагаются идеальными, т. е. такими, трение в которых отсутствует. Нагрузка Р приложена в узле А. Поэтому стержни будут испытывать только продольные (растягивающие или сжимающие) усилия, т.е. в поперечныхсеченияхстержней возникает только один внутренний силовой фактор - продольная сила N.
1. Для определения усилий рассмотрим равновесие узла А (рис. 2.34), к которому приложены нагрузка Р и два неизвестных усилия N1, и N2, действующие со стороны стержней АВ и АС и направленные вдольих осей.
При определении неизвестныхусилий в стержнях обычно принято считатьих растянутыми и соответственно этому направлять векторы сил от узла. Знак плюс в решении для усилия будет подтверждать правильность сделанного предположения о направлении усилия, а знак минус укажет на то, что в действительности усилие направлено противоположно и соответствующий стержень сжат.
Полагая оба стержня растянутыми, направим усилия N1, и N2 так,какпоказано на рис.2.34. Для плоской системы сил, пересекающихся в одной точке, как известноиз курса теоретической механики, можно составить только два независимых уравнения равновесия - в виде сумм проекции всех сил на две оси, не параллельные друг другу.
В качестве такихосей выберем оси Х и Y (рис. 2.34). Тогда уравнения равновесия представятся в виде:
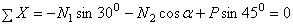 ;
;
 . (1)
. (1)
Из этой системы (1) можно было бы определить неизвестные усилия N1, и N2, если бы были известны значения  и
и 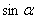 . Определим эти величины. Для этого рассмотрим данную стержневую систему (рис. 2.34). Из точки А опустим перпендикуляр АD на прямую ВС, получим два прямоугольных треугольника
. Определим эти величины. Для этого рассмотрим данную стержневую систему (рис. 2.34). Из точки А опустим перпендикуляр АD на прямую ВС, получим два прямоугольных треугольника 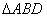 и
и 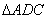 .
.

Рис.2.35
Из треугольника ABD определим AD:
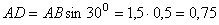 м.
м.
Из треугольника ADG получим:
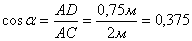
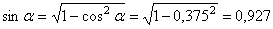 .
.
Теперь определим неизвестные усилия N1, и N2 из системы двух линейных уравнений (1). Перепишем уравнения в следующем виде:
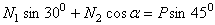 ;
;
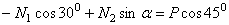 .
.
Решим эту систему используя метод Крамера
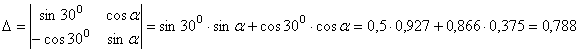 .
.
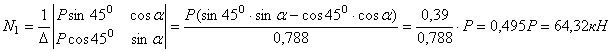 .
.
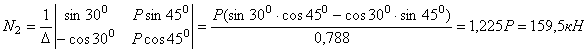 .
.
2. Определим нормальные напряжения, действующие в стержнях.
Напряжения в стержнях определяются по формуле
 .
.
Для первого стержня
 ,
,
для второго стержня
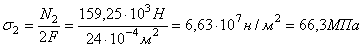 .
.
3. Найдем абсолютную и относительную деформации стержней.
Абсолютная деформация стержня длиной l равна:
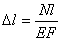 .
.
Абсолютная деформация первого стержня
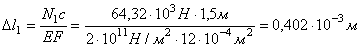 .
.
Абсолютная деформация второго стержня
 .
.
Относительную деформацию определим из закона Гука
 .
.
Относительная деформация первого стержня
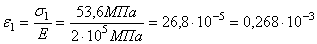 ,
,
Относительная деформация второго стержня
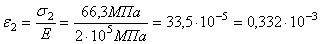 .
.
Дата добавления: 2015-08-08; просмотров: 1273;
