Поле равномерно заряженной сферы

Исследуем поле, созданное сферической поверхностью радиуса R, по которой равномерно распределен заряд 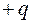. Из условия симметрии следует, что линии напряженности направлены радиально (рис. 30.1).

Изобразим сферу радиуса 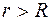, центр которой совпадает с центром заряженной сферы. Во всех точках этой сферы напряженность одинакова и линии напряженности перпендикулярны к ней. По этой причине поток вектора напряженности через сферу радиуса r равен

.

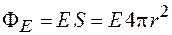Согласно теореме Гаусса

.

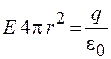Отсюда находим

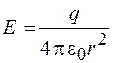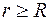( ). (30.1)

Полученная формула совпадает с формулой напряженности поля точечного заряда. Следовательно, поле равномерно заряженной сферы во внешней области таково, как если бы оно создавалось точечным зарядом, находящимся в центре сферы.

Если выбранная сфера имеет радиус 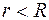, то заряд внутри нее равен нулю и напряженность поля тоже равна нулю.

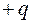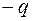Используя принцип суперпозиции, можно показать, что поле двух концентрических сфер с зарядами и (сферического конденсатора) сосредоточено в зазоре между поверхностями. Напряженность поля в зазоре определяется по формуле (30.1).

Если заряд распределен по объему шара равномерно с объемной плотностью заряда 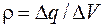, то напряженность поля за пределами шара рассчитывается по формуле (30.1). Напряженность поля внутри заряженного шара из расчетов на основании теоремы Гаусса оказывается прямо пропорциональной расстоянию от центра шара. Единица объемной плотности заряда - кулон на метр в кубе (Кл/м³). Поля зарядов, распределенных по объему, учитываются в электровакуумных приборах.