Поле бесконечной равномерно заряженной плоскости

Рассмотрим поле, созданное бесконечно протяженной плоскостью, заряженной равномерно с поверхностной плотностью заряда s. Эта величина характеризует распределение заряда по поверхности и численно равна заряду, приходящемуся на единицу площади:

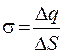, (27.1)

Полагая, что заряд плоскости положительный, определим направление линий напряженности. Из соображений симметрии следует, что точечный пробный заряд будет отталкиваться от бесконечной заряженной плоскости, в каком бы месте он ни располагался. Это означает, что линии напряженности направлены перпендикулярно плоскости (рис. 27.1).

Если выбрать две точки, расположенные симметрично относительно плоскости, то напряженность поля в этих точках по модулю будет одинакова. Для определения напряженности поля по теореме Гаусса выберем замкнутую поверхность цилиндра с образующими, перпендикулярными к плоскости, и основаниями площадью DS, расположенными параллельно плоскости и симметрично относительно нее (рис. 27.2). Такая форма поверхности упрощает вычисление потока: через боковую поверхность поток равен нулю, так как 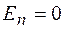, а поток через каждое основание равен 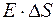, поскольку для них .

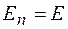Результирующий поток равен 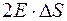. Заряд внутри поверхности равен 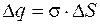, и в соответствии с теоремой Гаусса можно записать

_.

Отсюда находим

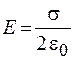. (27.2)

В полученную формулу не входит расстояние, следовательно, на любом расстоянии от плоскости значение напряженности одинаково.

Формулой (27.2) можно пользоваться и для поля плоскости конечных размеров, если расстояние от неe до точек поля, где рассчитывается напряженность, много меньше линейных размеров плоскости.

Если заряженная плоскость находится в среде с относительной диэлектрической проницаемостью e, то напряженность поля рассчитывается по формуле

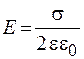. (27.3)