Поле равномерно заряженного цилиндра

Рассмотрим достаточно длинную цилиндрическую поверхность радиуса R, по которой равномерно распределен положительный заряд q (рис. 29.1).

Распределение заряда по длине цилиндра характеризуется линейной плотностью заряда

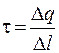, (29.1)

где Δq - заряд на отрезке Δl.

Единицей линейной плотности заряда является кулон на метр (Кл/м).

Размещая в разных точках поля пробный заряд, можно обнаружить, что действующие на него силы всегда направлены от цилиндра и перпендикулярны его оси. Это означает, что вектор напряженности в любой точке электрического поля направлен радиально. Из соображений симметрии следует так же, что в равноудаленных от оси цилиндра точках значение напряженности одинаково. Для расчета напряженности с применением теоремы Гаусса следует выбрать замкнутую поверхность такой формы, чтобы вычисление потока через отдельные ее участки выполнялось по возможности проще.

Наиболее удобны случаи, когда участок поверхности перпендикулярен линиям напряженности (тогда 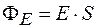) или параллелен им (тогда 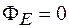). Исходя из этого в качестве поверхности для теоремы Гаусса целесообразно взять поверхность цилиндра, коаксиального с заряженным цилиндром. Радиус выбранного цилиндра равен r, а высота Δl. Поток вектора напряженности через поверхность этого цилиндра будет

.

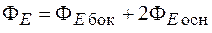Поток через основания 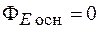, так как основания параллельны линиям напряженности, а поток через боковую поверхность 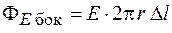. Следовательно, поток через замкнутую поверхность

.

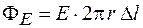Внутри цилиндра содержится отрезок заряженной поверхности высотой Δl, на котором распределен заряд 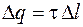. По теореме Гаусса для выбранной поверхности

.

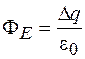Тогда получаем

.

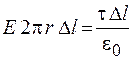Отсюда находим

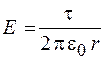, (r ³ R). (29.2)

Если 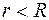(точка внутри заряженного цилиндра), то рассматриваемая поверхность не содержит внутри заряда, и потому

,

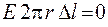откуда получаем

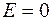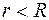, ( ). (29.3)

Таким образом, напряженность электрического поля заряженной цилиндрической поверхности максимальна на поверхности, внутри равна нулю, а вне ее убывает обратно пропорционально расстоянию от оси.

На основе принципа суперпозиции можно рассчитать поле двух коаксиальных цилиндрических поверхностей, заряженных с одинаковой по модулю, но противоположной по знаку линейной плотностью зарядов (рис. 29.2). В случае бесконечно длинных цилиндров ( 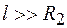) поле локализовано только в зазоре между цилиндрами и напряженность его определяется формулой (29.2). Такая система называется цилиндрическим (трубчатым) конденсатором. При наличии в конденсаторе диэлектрика напряженность поля между цилиндрами равна

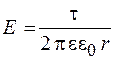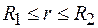( ). (29.4)