Волны. Плоские и сферические волны

Волновые процессы наблюдаются в упругих средах. Под упругой средой понимают среду, между частицами которой действуют упругие силы. Если какую либо частицу среды заставить совершать колебания, то за счет действия упругих сил в колебательное движение приходят сначала ближайшие к ней частицы, затем соседние с этими частицами и т. д. Так в колебательный процесс вовлекаются все новые и новые частицы, то есть в среде распространяется упругая волна. Этот процесс сопровождается переносом энергии от источника колебаний, причем переноса частиц в направлении движения волны не происходит – они совершают колебания около своих положений равновесия.

Различают продольные и поперечные волны. В продольной волне частицы среды совершают колебания вдоль вектора скорости распространения волны, а в поперечной – перпендикулярно к нему.

Введем характеристики, описывающие волновой процесс, на примере гармонической волны, в которой частицы среды совершают гармонические колебания около своих положений равновесия с циклической частотой ω.

1. Фронт волны – геометрическое место точек, до которых дошел волновой процесс.

2. Волновая поверхность – геометрическое место точек, колеблющихся в одинаковой фазе.

3. Период волны – время одного полного колебания частиц среды.

4. Длина волны λ – расстояние, которое проходит волна за один период, или минимальное расстояние между частицами среды, совершающими колебание с разностью фаз ∆φ = 2π.

Форма волновой поверхности и фронта волны зависят от условий возникновения и распространения волны. По виду волновых поверхностей выделяют плоские и сферические волны.

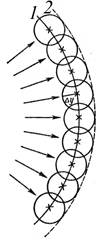
Часто при решении задач о распространении волн надо строить волновой фронт для некоторого момента времени по волновому фронту, заданному для начального момента времени. Это можно сделать с помощью метода, называемого принципом Гюйгенса. Согласно Гюйгенсу, каждая точка среды, до которой дошла волна, становится источником вторичных волн, и фронт каждой вторичной волны представляет собой сферу, огибающая фронтов вторичных волн определяет новое положение фронта волны.На рис. 1.1 фронт волны в некоторый момент времени t занимает положение 1, а через промежуток времени ∆t – положение 2.

Выведем уравнение плоской гармонической волны, распространяющейся в положительном направлении оси Ох. Как известно, в плоскости фронта волны – уОz – и параллельных ей плоскостях, все частицы совершают колебания в одинаковых фазе, поэтому в уравнении волны будет отсутствовать зависимость от координат у и z: ξ(х, у, z, t) = ξ(х, t). Пусть в момент времени t = 0 частицы с координатой х = 0, расположенные в плоскости уОz, начинают совершать колебания по закону

ξ(0, t) = А cos (ωt + φ₀). (1.1)

Частицы с координатой х > 0 начнут совершать колебания только после прихода к ним волны. Для этого требуется время τ = х/v, и поэтому уравнение колебаний для таких точек примет вид:

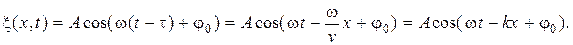(1.2)

Уравнение (1.2) представляет собой уравнение плоской гармонической волны, распространяющейся в положительном направлении оси Ох. В эту формулу входит волновое число k, которое связано с циклической частотой ω, скоростью распространения волны 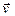и ее длиной волны соотношением

.(1.3)

Формула (1.3) определяет модуль волнового числа 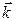.Направление вектора 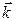совпадает с направлением скорости распространения бегущей волны.

Покажем, что входящая в формулу (1.2) скорость 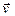волны представляет собой скорость движения фиксированного значения фазы волны – фазовую скорость. Действительно,

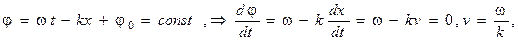(1.4)

что согласуется с формулой (1.3).

Волновым уравнением называют уравнение, решением которого является уравнение волны ξ(х, у, z, t). Найдем волновое уравнение для волновой функции (1.2). Если взять частные производные по координате х и времени t от ξ(х, у, z, t):

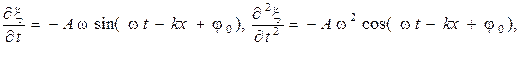
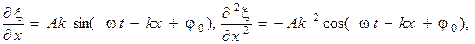
то тогда волновое уравнение принимает вид:

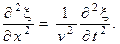(1.5)

Оказывается, что решением этого уравнения, кроме плоской гармонической волны, бегущей в положительном направлении оси Ох, является также плоская гармоническая волна, распространяющаяся в отрицательном направлении оси Ох

ξ(х, t) = A cos (ωt + kx +φ₀).

Для плоской гармонической волны, распространяющейся в произвольном направлении, которое можно задать радиусом-вектором 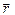,уравнение волны и волновое уравнение запишутся следующим образом

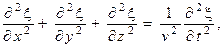(1.6)

ξ(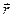, t) = Acos(ωt- 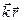+φ₀). (1.7)

Можно показать, что волновое уравнение (1.6) удовлетворяет также и уравнению сферической волны

ξ(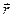, t) = A(r) cos (ωt - 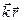+φ₀). (1.8)

Это уравнение отличается от уравнения плоской гармонической волны тем, что для сферической волны амплитуда А будет зависеть от расстояния rмежду точечным источником колебаний и рассматриваемой точкой в пространстве, а именно амплитуда сферической волны обратно пропорциональна расстоянию r.

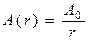, (1.9)

где А₀ – амплитуда волны на расстоянии 1 м от источника сферической волны.