Групповая скорость волны

Все реальные волны в той или иной степени отличаются от синусоидальных волн, так как энергия колебательного движения частично превращается в другие виды энергии, что ведет к уменьшению амплитуды колебаний по мере распространения волны. Уравнение плоской реальной волны можно записать в такой форме:

ξ(х, t) = А₀ е^-γх cos(ωt– kx+φ₀), (13.11)

где A₀ е^-γх– амплитуда волны, γ– коэффициент затухания. Эту волну можно представить как волну, полученную от наложения двух или большего количества синусоидальных волн с близкими частотами. Такую несинусоидальную волну называют группой волн или волновым пакетом.

В качестве примера рассмотрим простейший волновой пакет, образованный двумя плоскими продольными синусоидальными волнами, распространяющимися вдоль оси Ох. Пусть амплитуды этих волн одинаковы, начальные фазы φ₁₀= φ₂₀ = 0, а частоты и волновые числа несколько различны, но близки друг к дугу:

ξ₁ = A₀cos (ω₁t – k₁x ),

ξ₂ = A₀cos (ω₂t – k₂x ).

Для результирующей волны

ξ = ξ₁ + ξ₂ = 2А₀ cos(∆ωt - ∆kx) cos(ωt - kx),

где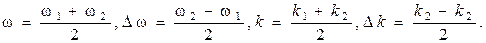

Таким образом, результирующая волна является плоской волной, циклическая частота ωи волновое число kкоторой равны полусумме соответственно циклических частот и волновых чисел синусоидальных волн, образующих пакет. Однако амплитуда этой волны не постоянна, а зависит от координаты хи времени t:

A= 2A₀ cos (∆ωt - ∆kx),

где ∆ωt- ∆kx= φ_А – фаза амплитуды распространяющейся волны. Дифференцируя выражение для φ_Ав предположении, что φ_А= const, получим:

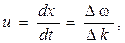
Или в пределе, когда ∆ω, а следовательно, и ∆kстремятся к нулю:

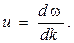
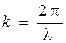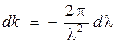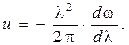Учитывая, что и : Так как 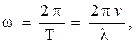где v– фазовая скорость волны, то

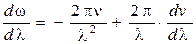и

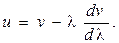(1.13)

Скорость uназывают групповой скоростью пакета волн. В случае отсутствия дисперсии волн в среде (т. е. когда dv/dλ= 0) их фазовые скорости vодинаковы и не зависят от λ. Поэтому в таких средах групповая скорость волн совпадает с их фазовой скоростью.

Лекция 2