Поток энергии волны

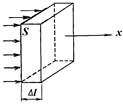При распространении волн частицы среды не переносятся вместе с волной. Процесс распространения волны в каком-либо направлении в среде сопровождается переносом энергии колебаний в этом направлении. Допустим, что S часть фронта плоской волны распространяющейся в направлении оси Ох в некоторый момент времени t (рис. 1.2). По истечении времени ∆t фронт волны переместится на расстояние ∆l = v∆t, вследствие чего частицы среды в объеме ∆V = S∆l приводятся в колебательное движение. Они будут обладать энергией

∆W = w∆V = wvS∆t,

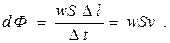
Величина dФ есть поток энергии волны через площадку S (S ориентируют перпендикулярно к направлению распространения волны). Плотностью потока энергии называют энергию, проходящую за единицу времени через единицу площадки, перпендикулярной к направлению распространения волны:

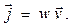(1.10)

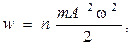Этот вектор называют вектором Умова и Пойнтинга. Учитывая, что где n– концентрация частиц среды, u_m= Аω– амплитуда скорости колебаний частиц среды, плотность энергии а j~ A². Распространяющиеся волны характеризуют понятием интенсивность волны I, которая пропорциональна среднему значению плотности потока, а, следовательно, I~ A².

В сферической волне, вызванной точечным источником колебаний, плотность потока энергии убывает обратно пропорционально квадрату расстояния от источника колебаний. Для доказательства допустим, что источник колебаний ежесекундно отдает в окружающую среду одну и ту же энергию, равную W. Эта энергия равномерно распределяется по шаровой поверхности фронта волны S= 4πr², поэтому через единицу площади этой поверхности в единицу времени проходит энергия

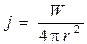, т. е. j~ 1/r², а А ~ 1/r(см. 1.9).