Стоячие волны. Стоячей волной называют волну, образующуюся при наложении двух встречных когерентных волн

Стоячей волной называют волну, образующуюся при наложении двух встречных когерентных волн. Рассмотрим случай наложения двух плоских волн, распространяющихся вдоль оси Ох в положительном ξ₁(х, t) и отрицательном ξ₂(х, t) направлениях:

ξ₁(х, t) = А cos(ωt - kx), ξ₂(х, t) = А cos(ωt + kx).

Для уравнения стоячей волны в соответствии с формулой сложения колебаний можно записать:

ξ_ст(х, t) = ξ₁ + ξ₂ = 2А cos kx cos ωt (2.6)

Из формулы (2.6) следует, что амплитуда стоячей волны

А_ст = | 2А cos kx | (2.7)

зависит от координаты х выбранной точки пространства, изменяясь от минимального значения, равного нулю (А_ст = 0), до максимального значения, равного 2А (А_ст = 2А).

Найдем координаты точек пространства х_п, в которых наблюдается максимальная амплитуда колебаний частиц среды, их называют пучностями стоячей волны, и координаты узлов стоячей волны (х_у), для них амплитуда колебаний частиц среды равна нулю:

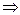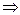
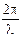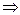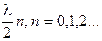А_ст = 2А coskx_п= ± 1 х_п = nπ х_п = (2.8)

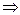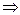
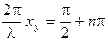
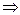
А_ст= 0 coskx_у= 0 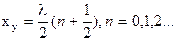(2.9)

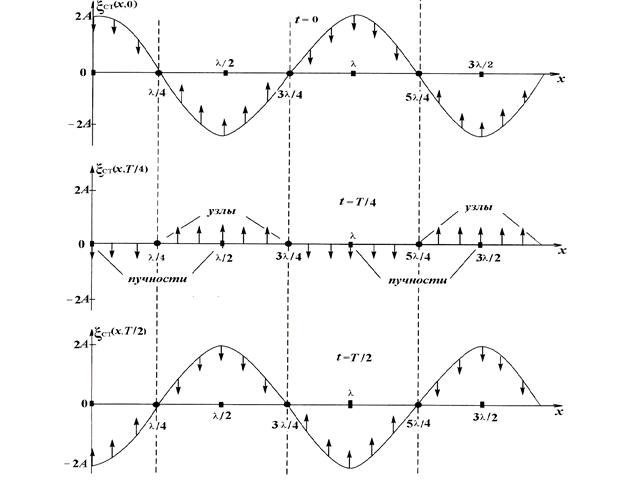
Из формул (2.8) и (2.9) следует, что расстояние между соседними узлами ∆х_у и соседними пучностями ∆х_пстоячей волны одинаково и равно ∆х = ∆х_п = ∆х_у = λ/2.

Стоячие волны обычно образуются при отражении бегущей волны от границы раздела двух сред. При этом возможны два случая. В первом при отражении волны от более плотной среды фаза волны изменяется на значение равное πи на границе раздела образуется узел стоячей волны. Во втором случае при отражении волны от менее плотной среды фаза волны не изменяется и на границе разделе образуется пучность стоячей волны.