Следствия из преобразований Лоренца. Одновременность событий в разных системах отсчета.Пусть в системе К в точках с координатами х1 и х2 происходят одновременно два события в момент времени t1 =

Одновременность событий в разных системах отсчета.Пусть в системе К в точках с координатами х₁ и х₂ происходят одновременно два события в момент времени t₁ = t₂ = b. В соответствии с преобразованиями Лоренца в системе К' этим событиям будут соответствовать моменты времени

.

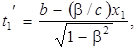
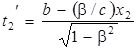Из данных формул видно, что в случае, если события в системе К пространственно разобщены (х₁ ≠ х₂), то в системе К' они не будут одновременными (t₁^' ≠ t₂^'). Знак разности t₂^' – t₁^' определяется знаком выражения (β/c)(x₁ – x₂); следовательно, в разных системах К' (при разных β) разность t₂^' – t₁^' будет различна по величине и может отличаться по знаку. Это означает, что в одних системах событие 1 будет предшествовать событию 2, в других системах, наоборот, событие 2 будет предшествовать событию 1. Заметим, что сказанное относится лишь к событиям, между которыми отсутствует причинная связь.

Продолжительность явления.Пусть в одной и той же точке с координатой х^' = асистемы К' происходит явление, которое начнется в момент времени t₁^' и закончится в момент времени t₂'. Согласно преобразований Лоренца этим событиям соответствуют в системе К моменты времени

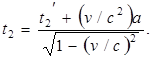Отсюда

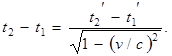
Введя обозначение t₂ – t₁ = ∆t и t₂^' – t₁^' = ∆t', получим формулу

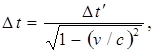(5.1)

которая связывает промежутки времени между двумя событиями, измеренные в системах К и К^'. Допустим, что оба события происходят с одной и той же частицей, которая покоится в системе К' и движется относительно системы К со скоростью v. Тогда ∆t'можно трактовать как промежуток времени, измеренный по часам, неподвижным относительно частицы, или, иными словами, измеренный по часам, движущимся вместе с частицей. Время, отсчитанное по часам, движущимся вместе с телом, называется собственное время этого тела и обозначается буквой τ. Таким образом, ∆t' = τ.С учетом этого формуле (5.1) можно придать вид

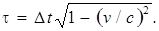(5.2)

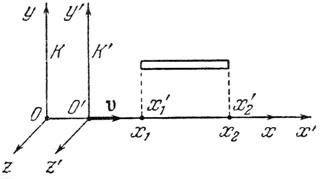
Длина тел в разных системах.Рассмотрим стержень, расположенный вдоль оси х'и покоящийся относительно системы отсчета К^' (рис. 5.1). Длина его в этой системе l₀ = x₂'- x₁^', где х₁^' и х₂^' – не изменяющиеся со временем t^' координаты концов стержня. Относительно системы К стержень движется со скоростью v. Для определения его длины в этой системе нужно отметить координаты концов стержня х₁ и х₂ в один и тот же момент времени t₁= t₂ = b. Их разность l = x₂ – x₁ дает длину стержня, измеренную в системе К. Чтобы найти соотношения между l₀ и l, следует взять ту из формул преобразований Лоренца, которая содержит х^', х и t.

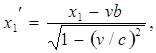
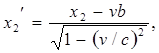откуда

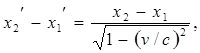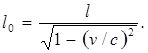или (5.3)

Таким образом, длина стержня l, измеренная в системе отсчета, относительно которой он движется, оказывается меньше длины l₀, измеренной в системе, относительно которой стержень покоится.

Заметим, что в направлении осей yи zразмеры стержня одинаковы во всех системах отсчета. Итак, у движущихся тел размеры их в направлении движения сокращаются тем больше, чем больше скорость движения. Это явление называют лоренцевым сокращением.