Релятивистское выражение для энергии

Найдем выражение для кинетической энергии материальной точки в релятивистской механике. Приращение dTкинетической энергии материальной точки при элементарном перемещении 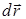равно работе ( 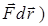, совершенной при этом перемещении силой 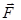, действующей на точку:

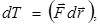
или

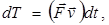
поскольку .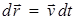

Из основного уравнения релятивистской динамики (5.6) следует, что

.

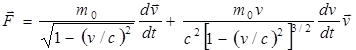Поэтому

.

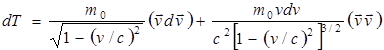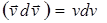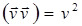Так как и , то

.

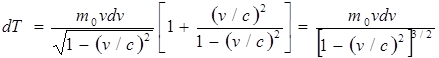С другой стороны, как видно из формулы (5.4),

.

Таким образом, при изменении скорости материальной точки изменение ее кинетической энергии и массы пропорциональны друг другу:

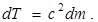(5.7)

Интегрирование полученного соотношения дает

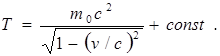
При v= 0, m= m₀ и Т= 0. Отсюда для константы получается значение, равное – m₀c². Следовательно, релятивистское выражение для кинетической энергии частицы имеет вид

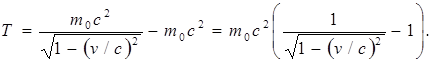(5.8)

В случае малых скоростей (v<< c) формулу (5.8) можно преобразовать следующим образом:

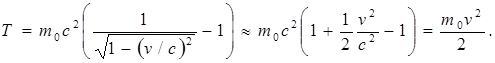
Мы пришли к ньютоновскому выражению для кинетической энергии частицы. Этого и следовало ожидать, поскольку при скоростях, много меньше скорости света, все формулы релятивистской механики должны переходить в соответствующие формулы ньютоновской механики.

Перепишем формулу (5.8) в следующем виде:

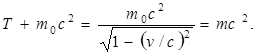
Анализируя это соотношение, Эйнштейн предположил, что полная энергия тела должна складываться из энергии его движения (кинетической) и энергии покоящегося тела (внутренней). Поэтому он отождествил второе слагаемое в этой формуле с внутренней энергией тела и назвал ее энергией покоя Е₀, а сумму (Т + m₀c²) – полной энергией тела Е:

Е₀ = m₀c²; Е = mc² . (5.9)

Нужно отметить, что энергия покоя и полная энергия не включают в себя потенциальной энергии тела во внешних полях.

Из выражений для импульса (5.5) и энергии (5.9) можно получить полезные формулы связи между ними:

;

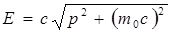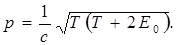
В классической физике

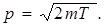
Лекция 6