Потенциальная энергия. Потенциал. Работа сил электрического поля

Взаимодействие между неподвижными зарядами осуществляется посредством электростатического поля: взаимодействуют не заряды, а один заряд в месте своего расположения взаимодействует с полем, созданным другим зарядом.

Покажем, что электростатическое поле является потенциальным. Для этого рассчитаем работу кулоновской силы при перемещении точечного положительного заряда q₂из точки1 в точку 2 (рис. 6.1б) в электрическом поле, созданным точечным зарядом q₁:

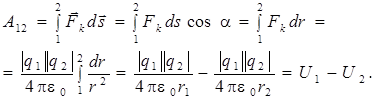(6.2)

Как видно из формулы (6.2), в окончательное выражение входят величины, описывающие только начальное и конечное положение заряда q₂, то есть работа сил поля не зависит от пути перехода из точки 1 в точку 2. Это означает, что кулоновская сила будет консервативной, а электрическое поле – потенциальное. В таком поле заряд q , помещенный в некоторую точку, обладает потенциальной энергией U.

На основании формулы (6.2) для U можно записать следующее выражение:

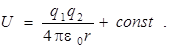(6.2а)

Как видно из выражения (6.2а), Uопределяется с точностью до постоянной величины. Для электростатического поля точечного заряда принято выбирать constтак, чтобы на бесконечно большом расстоянии между зарядами их взаимная потенциальная энергия обращалась в ноль. Следовательно,

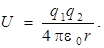(6.2б)

Из формулы (6.2б) видно, что отношение потенциальной энергии Uзаряда q к его величине не зависит от q и поэтому может служить энергетической характеристикой электростатического поля. Отношение U/q обозначается через φ и называется потенциалом электрического поля:

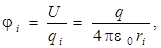(6.3)

где r_i – расстояние от точки поля, обладающего потенциалом φ_i, до заряда q, создающего поле.

Работу, совершенную электрическими силами при перемещении произвольного по величине заряда q можно выразить через разность потенциалов φ₁ и φ₂ в точках 1 и 2:

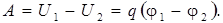(6.4)