Прямой, обратный и дополнительный коды чисел
В ЭВМ используется прямой, обратный и дополнительный коды чисел. Знак “+” кодируется нулем (0), “-” - единицей (1), которые записываются в дополнительном старшем разряде - знаковом разряде.
Возьмем целое число С = + Cn Cn-1 Cn-2 ...C1 C0 .
- Прямой код для целых чисел определяется:
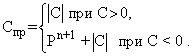
Для отрицательных двоичных чисел имеем:
C = 2 +ç-Cn Cn-1 ...C0 ç= 1.Cn Cn-1 ...C0,
где точкой отделен знаковый разряд.
Таким образом, для получения прямого кода числа надо в знаковый разряд записать 0 для положительных и 1 для отрицательных чисел.
C = +10110, Cпр = 0.10110;
C = -10110,
Cпр = 1.10110.
Сложение в прямом коде не вызывает затруднений, когда у слагаемых одинаковые знаки: сложить модули и сумме присвоить знак слагаемых. При вычитании чисел в прямом коде нужно сначала определить больший модуль, от него отнять меньший и результату присвоить знак большего модуля.
2. Обратный код определяется:
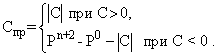
Для отрицательных двоичных чисел имеем:
Cобр = 2n+2 - 1 -ç-Cn Cn-1 …C0ç = 11…1 – 0.Cn Cn-1…C0= 1. 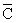 n
n 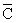 n-1…
n-1… 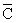 0,
0,
где 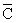 I = 1 при Ci = 0 и
I = 1 при Ci = 0 и 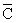 I = 0 при Ci = 1 .
I = 0 при Ci = 1 .
Таким образом, для представления чисел в обратном коде надо в знаковый разряд записать 0 или 1, для отрицательных чисел в значащие разряды нужно записать дополнение модуля исходного числа до наибольшего числа без знака, помещающегося в данных разрядах. Для двоичной системы счисления последнее означает, что в случае отрицательных чисел для получения обратного кода надо значение разрядов инвертировать: вместо 0 записать 1,вместо 1 – 0.
C = +10110, Cобр = 0.10110; С = -10110, Собр = 1.01001.
- Дополнительный код чисел определяется:
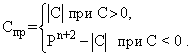
При представлении двоичного отрицательного числа в дополнительном коде в знаковый разряд надо записать 1, а цифровую часть заменить дополнением числа до 2n+1 .
Сравним выражения для представления обратного и дополнительного кода числа. Становится очевидно, что дополнительный код отрицательных чисел получается из обратного прибавлением единицы в младший разряд.
Cдоп = Собр +1, при С < 0 .
C = +10110, Cдоп = 0.10110; С = -10110, Сдоп = 1.01010.
Как можно увидеть, при вычислениях в ЭВМ в прямом и обратном коде может получиться как положительный, так и отрицательный нуль (+0, -0).
(+0)пр=0,00…0, (-0)пр=1,00..0;
(+0)обр=0,00…0, (-0)обр=1,11…1.
И только в дополнительном коде нуль представляется однозначно:
(+0)доп = 0,00…0, (-0)доп = 1,11…1+2-m = 0.
Нетрудно доказать, что (по модулю):
- Обратный код от обратного кода дает прямой код числа.
- Дополнительный код от дополнительного кода дает прямой код числа.
Дата добавления: 2015-08-08; просмотров: 1109;
